Теорема Лиувилля

[MChagall]

Имеются следующие задачи.
1) Доказать теорему Лиувилля следующим образом: вычислить и оценить $$\int\limits_{\left\lvert z\right\rvert=R}^{}\frac{f(z)dz}{(z-a)(z-b)}; \left\lvert a\right\rvert, \left\lvert b\right\rvert< R$;
2) Для целой функции $f(z)$ и $\forall z\in \mathbb{C}$ известно, что $\left\lvert f(z)\right\rvert \leqslant M(1+\left\lvert z\right\rvert)^n$, где $M$ и $n>0$ - константы. Показать, что $f$ - многочлен, и что $deg f \leqslant n$;
3) $P(z)=z^n+...$. И $\max\limits_{\left\lvert z\right\rvert=1}\left\lvert P(z)\right\rvert\leqslant 1$. Доказать, что $P(z)=z^n$.

1) У меня получилось $$\int\limits_{\left\lvert z\right\rvert=R}^{}\frac{f(z)dz}{(z-a)(z-b)}=2 \pi i \frac{f(a)-f(b)}{a-b}$. При стремлении $b$ к $a$ получается $f'(a)$. Пусть $\left\lvert f(z)\right\rvert\leqslant M$. Пытаюсь оценить, хочу что-то вроде $\leqslant \frac{M}{R}$.
Получается вот что: $\int\limits_{\left\lvert z\right\rvert=R}^{}\frac{f(z)dz}{(z-a)(z-b)}\leqslant M\int\limits_{\left\lvert z\right\rvert=R}^{}\frac{dz}{(z-a)(z-b)}=\frac{M}{a-b}(\int\limits_{\left\lvert z\right\rvert=R}^{}\frac{dz}{(z-a)}-\int\limits_{\left\lvert z\right\rvert=R}^{}\frac{dz}{(z-b)})=$$\frac{M}{a-b}(2 \pi i - 2\pi i)=0$. Что-то не очень мне нравится. Где у меня ошибка? И как тогда оценить?
2) Из оценки модуля следует, что главная часть ряда Лорана в $\infty$ содержит степени не выше $n$, значит там полюс. А целая функция с полюсом в бесконечности - полином. Ну и степень следует из того же ряда. Вроде, решение-то есть, но есть вопросы: а) зачем нужна такая оценка, разве не подойдёт такая $\left\lvert f(z)\right\rvert \leqslant M \left\lvert z\right\rvert^n$?
б) задача из листка до рядов (на интегралы, принцип максимума модуля и т.д.). Причём то, что степень не выше $n$ у меня получилось сделать так $\left\lvert f^{(n+1)}(z_0)\right\rvert\leqslant \frac{M(1+\left\lvert z\right\rvert)^n (n+1)!}{R^{n+1}}$ (использую, что если $\left\lvert z-z_0\right\rvert<R$, то $\left\lvert z\right\rvert\leqslant \left\lvert z_0\right\rvert+R$). И при $R\to \infty$ получаем, что $n+1$-я производная и выше равны нулю. А вот как без рядов доказать, что это полином? Возможно ли это?

[thething]

MChagall в сообщении #1302592 писал(а):

И как тогда оценить?

Во-первых, навесить модули, а во-вторых, в знаменателе -- модули разности

Во второй задаче применить неравенство Коши для коэффициентов ряда Лорана

MChagall в сообщении #1302592 писал(а):

разве не подойдёт такая $\left\lvert f(z)\right\rvert \leqslant M \left\lvert z\right\rvert^n$?

И так и так можно

MChagall в сообщении #1302592 писал(а):

при $R\to \infty$ получаем, что $n+1$-я производная и выше равны нулю

А у какой функции все производные с какого-то номера тождественно обращаются в нуль? (ну, типа, что если дифур решить?)

[MChagall]

thething в сообщении #1302598 писал(а):

Во-первых, навесить модули

$\left\lvert\int\limits_{\left\lvert z\right\rvert=R}^{}\frac{f(z)dz}{(z-a)(z-b)}\right\rvert\leqslant M\left\lvert\int\limits_{\left\lvert z\right\rvert=R}^{}\frac{dz}{(z-a)(z-b)}\right\rvert=\frac{M}{\left\lvert a-b\right\rvert}\left\lvert\int\limits_{\left\lvert z\right\rvert=R}^{}\frac{dz}{(z-a)}-\int\limits_{\left\lvert z\right\rvert=R}^{}\frac{dz}{(z-b)}\right\rvert=$$\frac{M}{\left\lvert a-b\right\rvert}\left\lvert2 \pi i - 2\pi i\right\rvert=0$.

Где ошибаюсь?

[g______d]

В первом неравенстве.

[MChagall]

g______d в сообщении #1302626 писал(а):

В первом неравенстве

Тогда где у меня заблуждение?
$g(z)=\frac{f(z)}{(z-a)(z-b)}; h(z)=\frac{M}{(z-a)(z-b)}$. И $\forall z\ne a, b \left\lvert g(z)\right\rvert\leqslant \left\lvert h(z)\right\rvert$ $\Rightarrow$ $\left\lvert\int\limits_{\left\lvert z\right\rvert=R}^{}g(z)dz\right\rvert\leqslant \left\lvert\int\limits_{\left\lvert z\right\rvert=R}^{}h(z)dz\right\rvert$

[g______d]

MChagall в сообщении #1302633 писал(а):

Тогда где у меня заблуждение?

В последней импликации.

[MChagall]

thething в сообщении #1302598 писал(а):

Во-первых, навесить модули, а во-вторых, в знаменателе -- модули разности

Не пойму, что в знаменателе делать. Вот, как ещё вижу $\left\lvert\int\limits_{\left\lvert z\right\rvert=R}^{}\frac{f(z)dz}{(z-a)(z-b)}\right\rvert\leqslant L 2\pi R$, где $L=\max\limits_{\left\lvert z\right\rvert=R}\left\lvert\frac{f(z)}{(z-a)(z-b)}\right\rvert$. Но чему равен $L$?

[Otta]

MChagall

MChagall в сообщении #1302633 писал(а):

Тогда где у меня заблуждение?...
$\left\lvert g(z)\right\rvert\leqslant \left\lvert h(z)\right\rvert\Rightarrow\left\lvert\int\limits_{\left\lvert z\right\rvert=R}^{}g(z)dz\right\rvert\leqslant \left\lvert\int\limits_{\left\lvert z\right\rvert=R}^{}h(z)dz\right\rvert$

Воспользуйтесь "правильным" неравенством вместо этого, как можно более точно оценивая, не так грубо, как в последнем посте, и все получится.

[vpb]

Otta в сообщении #1302653 писал(а):

как можно более точно оценивая, не так грубо, как в последнем посте, и все получится

Мне кажется, той оценки достаточно, только еще само $L$ оценить надо. А как там можно еще более точно?

MChagall в сообщении #1302592 писал(а):

зачем нужна такая оценка, разве не подойдёт такая $\left\lvert f(z)\right\rvert \leqslant M \left\lvert z\right\rvert^n$?

Нет, не подойдет.

Конечно, говоря формально, утверждение, что из $|f(z)|\leq M|z|^n$ $\forall\ z\in {\mathbb C}$ следует, что $f(z)$ --- многочлен степени $\leq n$, верно. Но это утверждение существенно более слабое, чем то, что требуется в задаче, поскольку условие $|f(z)|\leq M|z|^n\ \forall z\in{\mathbb C}$ сильнее, чем $|f(z)|\leq M(1+|z|)^n\ \forall z\in{\mathbb C}$. Условие задачи означает, что функция целая и на бесконечности растет не быстрее, чем $|z|^n$. 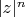А условие $|f(z)|\leq M|z|^n\ \forall z\in{\mathbb C}$ означает, что она вдобавок еще и в нуле имеет нуль порядка не менее $n$.

Ситуаций, когда применимо исходное утверждение задачи, море. А если условие усилить, заменив на $|f(z)|\leq M|z|^n\ \forall z\in{\mathbb C}$, получится утверждение малосодержательное, фактически с нулевой областью применения. (Заметим в скобках, что если $|f(z)|\leq M|z|^n\ \forall z\in{\mathbb C}$, то на самом деле $f(z)=Az^n$, для некоторого $A$ с $|A|\leq M$.)

[Otta]

vpb в сообщении #1302658 писал(а):

Мне кажется, той оценки достаточно, только еще само $L$ оценить надо. А как там можно еще более точно?

Оценив само $L$ Забавно, когда считаешь с другого конца, своих в лицо не узнаешь ))

[MChagall]

Otta в сообщении #1302659 писал(а):

Оценив само $L$

Вот что ещё получилось $\left\lvert \frac{f(z)}{(z-a)(z-b)}\right\rvert\leqslant\frac{M}{\left\lvert z-a\right\rvert \left\lvert z-b\right\rvert}\leqslant\frac{M}{(R-\left\lvert a\right\rvert)(R- \left\lvert b\right\rvert)}$
И получается $\left\lvert\lim\limits_{a\to b}^{}\frac{2\pi(f(a)-f(b))}{a-b}\right\rvert\leqslant\frac{2\pi M}{R(1-\frac{\left\lvert a\right\rvert}{R})(1-\frac{\left\lvert b\right\rvert}{R})}$, то есть $\left\lvert f'(b)\right\rvert\leqslant\frac{M}{R(1-\frac{\left\lvert a\right\rvert}{R})(1-\frac{\left\lvert b\right\rvert}{R})}$. Левая часть от $R$ не зависит, следовательно производная нулевая и функция константа. Верно всё?

[thething]

MChagall в сообщении #1302672 писал(а):

Вот что ещё получилось $\left\lvert \frac{f(z)}{(z-a)(z-b)}\right\rvert\leqslant\frac{M}{\left\lvert z-a\right\rvert \left\lvert z-b\right\rvert}\leqslant\frac{M}{(R-\left\lvert a\right\rvert)(R- \left\lvert b\right\rvert)}$

А чего так долго-то досюда добирались? Вроде не впервой уже

MChagall в сообщении #1302672 писал(а):

И получается $\left\lvert\lim\limits_{a\to b}^{}\frac{2\pi(f(a)-f(b))}{a-b}\right\rvert\leqslant\frac{2\pi M}{R(1-\frac{\left\lvert a\right\rvert}{R})(1-\frac{\left\lvert b\right\rvert}{R})}$

Это любопытный предельный переход.. А может, всё-таки по $R$..

[MChagall]

thething в сообщении #1302692 писал(а):

А чего так долго-то досюда добирались?

Да не знаю, вроде, и правда не сложный переход.

thething в сообщении #1302692 писал(а):

всё-таки по $R$

$\lim\limits_{R\to \infty}^{}\left\lvert\frac{2\pi(f(a)-f(b))}{a-b}\right\rvert\leqslant\lim\limits_{R\to \infty}^{}\frac{2\pi M}{R(1-\frac{\left\lvert a\right\rvert}{R})(1-\frac{\left\lvert b\right\rvert}{R})}=0 \Rightarrow f(a)=f(b) \forall a,b\in\mathbb{C} $ $ \Rightarrow f(z)=\operatorname{const}$. И никаких производных не нужно. Вроде, верно?

[MChagall]

По поводу задачи 3 особых мыслей и нет. Возможно, надо показать, что если $P(z)=z^n+...$, то на окружности $\left\lvert z\right\rvert=1$ найдётся точка $z_0$, такая, что $P(z_0)>1$. Но как это показать? Ввести $z=e^{i\varphi}$ ? $z^n$ оставит точку на окружности. А дальше?

[thething]

Поясните, что скрывается за многоточием?