Разбираюсь с темой интегралов от функций комплексного переменного.
1) Найти

, где

2) Для произвольного пути, соединяющего 0 и 1 и не проходящего через

найти
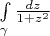
3)

,

. Найти

Для 1) вроде так:

Правильно ли я сделал?
Для 2) я так понимаю уже зависит от пути. Путь, гомотопный

даёт

.
А пути, которые не гомотопны данному, наверное, дают что-то другое. И как здесь быть?
Для 3) есть пара мыслей. У

на

существует первообразная

. Поэтому

Далее

. Если это верно, то что делать дальше?
Или напрашивается переход к полярным координатам

. И опять: что дальше?