Я просил Вас сформулировать признак, которым Вы пытались воспользоваться.
Теорема об этом признаке звучит так: Пусть даны два знакоположительных ряда
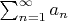
и
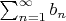
. Если для всех n выполняется неравенство

, то из сходимости ряда
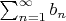
следует сходимость ряда
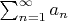
, а из расходимости ряда
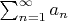
следует расходимость ряда
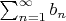
.
Этот признак не помог, зато помог предельный признак сравнения и я нашёл ответ о сходимости нужного ряда.
Но тут начал решать следующее задание и тут уже точно застрял.
Надо найти сходимость ряда

Примеров на логарифмы я вообще не видел ни разу.
Что я тут пробовал:
1. Найти сумму ряда: не знаю, как суммировать логарифмы, поэтому не подходит.
2. Признак сравнения, который описал выше использовать не могу, так как не знаю, с чем сравнить этот ряд, содержащий логарифм.
3. Предельный признак сравнения по той же причине не подходит.
4. Признак Даламбера вроде начал получаться, но ответа он не дал, так как получилось значение 1:
Распишу





5. Радикальный признак Коши пробовать не стал, так как думаю заранее, что не подойдет.
6. Интегральный признак Коши пробовал, но не смог использовать так как в ответе получался интегральный логарифм, который мы не изучали вообще и поэтому я не знаю, что с ним дальше делать

и дальше всё...
Других признаков я не знаю.