Задача на граф.

[an2ancan]

Здравствуйте, помогите разобраться:

Электрическая цепь представляет собой связный неориентированный граф без кратных ребер, в котором ребра (числом $N$) - это провода, а вершины - либо лампочки, либо единственный источник тока. На каждом ребре размещено реле. Лампочка горит, если существует путь, соединяющий ее с источником тока, вдоль которого все реле находятся в положении "включено". Известно, что ровно одно из реле бракованное и никогда не пропускает ток. Вы можете включать и отключать реле (и видите, горят ли лампочки). Изначально все выключатели находятся в положении "включено". Опишите способ нахождения неисправного реле за $O(N)$ операций включения-выключения.

Мое решение:
Пронумеруем вершины, источник тока примем за 0. выключим все реле, которые иду от источника тока, кроме одного (который ведет к лампочке 1). Если лампоча, к котроой ведет ребро (реле) не горит, то реле сломано, если горит, выключаем все реле, которые ведут от текущей лампы, кроме одного с наименеьшим номером (но с большим, чем номер текущей лампы). Процесс продолжается до тех пор, пока не останется ребер ведущих к лампочке с большим номером. Тогда мы возвращаемся на одну лампу назад и выключаем проверенное ребро, и включаем следующее ведущее к соседней лампе, но с большем индексом. В случае если таковых нет, возвращаемся назад.

Выходит, что каждое ребро (реле) мы выключаем - включаем не больше раза, т.е. сложность алгоритма - $O(n)$.

Поправьте, если я не прав, спасибо

[Pphantom]

Тема перемещена из форума «Computer Science» в форум «Карантин»
по следующим причинам:

- отсутствуют собственные содержательные попытки решения задачи.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.

[Pphantom]

Тема перемещена из форума «Карантин» в форум «Computer Science»

[Skeptic]

На схему не задано никаких ограничений, следовательно, могут встречаться реле, соединённые через лампочку последовательно. Если одно из реле не работает, то его не определить операциями включения-выключения.

[worm2]

По-моему, формулировка у задачи неудачная. Все знают, что к любой нагрузке в цепи должны подходить два провода: плюс и минус или ноль и фаза. А тут вдруг граф: один-единственный провод от источника тока до лампочки — и она работает. Как??? От этого наступает ступор, и время тратится непродуктивно.

-- Пт дек 15, 2017 17:52:53 --

Можно попробовать "спасти" задачу тем, что объявить: все лампочки одним контактом заземлены, а другим — этими проводами соединяются с соседними лампочками или источником тока (фазой).

[an2ancan]

Ну а все-таки, если представить, что задача придумвывалась не элктриками, ну или если представить, что все лампочки заземлены, вышеуказанный алгоритм верен или нет?

[worm2]

Я его не понял, так что не могу сказать. Своего алгоритма тоже не придумал.

[B@R5uk]

an2ancan в сообщении #1274181 писал(а):

Электрическая цепь представляет собой связный неориентированный граф без кратных ребер, в котором ребра (числом $N$) - это провода, а вершины - либо лампочки, либо единственный источник тока. На каждом ребре размещено реле. Лампочка горит, если существует путь, соединяющий ее с источником тока, вдоль которого все реле находятся в положении "включено". Известно, что ровно одно из реле бракованное и никогда не пропускает ток. Вы можете включать и отключать реле (и видите, горят ли лампочки). Изначально все выключатели находятся в положении "включено". Опишите способ нахождения неисправного реле за $O(N)$ операций включения-выключения.

Лучше переформулировать так:

Задан граф, рёбра которого можно разрывать/удалять и снова соединять/добавлять (но нельзя добавлять новых, не существующих в исходном графе). Одна из вершин графа является особенной — корнем. Ко всем остальным вершинам привязана особая функция, которая может мгновенно определить, есть ли связь этой вершины с корнем (по не разорванным/ не удалённым рёбрам). Одно ребро в графе "испорчено", то есть всегда разорвано/удалено, но этого не видно. Удаляя/разрывая и добавляя/соединяя рёбра и ориентируясь на показания функций в каждой вершине найти это самое "испорченное" ребро.

С электрической точки зрения всё правильно, если считать, что один конец каждой лампочки сидит на земле, а другой — подключён к вершине. С источником аналогично. Вообще, эта задача больше для раздела "Помогите решить/разобраться" подходит.

[nds]

Рисуем связный неориентированный граф без кратных ребер.

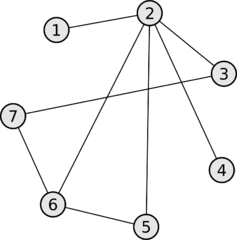
Картинки другой нет, поэтому, я изменю нумерацию. Пусть 2 это источник тока, а 1, 3-7 -- это лампочки.
Начальное условие: Изначально все выключатели находятся в положении "включено".

Дальше стоит всё же определиться со схемой. Лампы имеющие 2 ребра можно зажечь двумя путями. Если такие есть, то задача усложняется.
Потому что изначально все лампочки могут гореть даже если есть неисправное реле.

Если есть только лампы типа $1$ и $4$, то операций вообще нет никаких, реле соединяющее не горящую лампочку с горящей и есть неисправное.

Если же ребер несколько, как $3, 5, 7$, то:
а) если 1 лампочка не горит, то количество операций $=$ количество ребер $-1$
б) все лампочки горят: Отключаем по очереди все реле к лампочкам с рёбрами больше 1, ждём когда лампочка(ки) потухнут и исследуем дублирующие реле вокруг не горящих лампочек.

Дальше чистая математика -- считайте сами.

Но это при условии: Лампочка горит, если существует путь, соединяющий ее с источником тока, вдоль которого все реле находятся в положении "включено". Т.е. все лампочки соединяются параллельно.

-- 19.12.2017, 20:02 --

B@R5uk в сообщении #1276535 писал(а):

С электрической точки зрения всё правильно, если считать, что один конец каждой лампочки сидит на земле, а другой — подключён к вершине. С источником аналогично.

Ребро может состоять из двух проводов, или двух реле, как угодно. Тогда каждую горящую лампочку можно рассматривать как источник тока, к которому подключаются другие лампочки.

[B@R5uk]

nds в сообщении #1276537 писал(а):

Ребро может состоять из двух проводов, или двух реле, как угодно.

Материала потребуется больше, но работать тоже будет.

Вообще, я бы строил алгоритм следующим образом. Разбил бы множество вершин на "слои" по степени удаления от корня. Затем поочерёдно искал бы сломанное ребро между $n-1$-ым и $n$-ым слоями, между вершинами $n$-го слоя, затем увеличивал бы $n$ на единицу и повторял с начала, пока не найдётся ребро или не будут перебраны все рёбра. Можно это делать и в обратном порядке, но тогда в самом начале нужно некоторое нетривиальное с алгоритмической точки зрения приготовление, локализующее сломанное ребро, если часть лампочек при всех включенных реле не горит. При прямом ходе, ничего проверять не надо и алгоритм получается значительно более простым.

[Sender]

Оставляем включённым какое-нибудь остовное дерево с корнем в источнике. В дереве сразу видно, какое ребро нерабочее, т.к. путь от корня до любой вершины единственен. Если сразу не нашли, поочерёдно перебираем оставшиеся рёбра, по одному включая их и разрывая получающийся при этом цикл в произвольном месте.

[nds]

an2ancan
А откуда вообще задача? Электротехника?
Ваша цель задачу правильно поставить или её решить?

[an2ancan]

nds в сообщении #1276552 писал(а):

an2ancan
А откуда вообще задача? Электротехника?
Ваша цель задачу правильно поставить или её решить?

Нет, задача из одного вступительного варианта в заведение по подготовке специалистов по анализу данных, так что там главное описать алгоритм.

Sender в сообщении #1276550 писал(а):

Оставляем включённым какое-нибудь остовное дерево с корнем в источнике. В дереве сразу видно, какое ребро нерабочее, т.к. путь от корня до любой вершины единственен. Если сразу не нашли, поочерёдно перебираем оставшиеся рёбра, по одному включая их и разрывая получающийся при этом цикл в произвольном месте.

Ваше решение, на мой дилетантский взгляд, кажется вполне приемлимым.

Сложность поиска оставного дерева (с у четом, что все веса равны) $O(N)$ (можно создать множество, пройтись по ребрам. Если обе вершины пренадлежат множеству, не добавлять ребро к оставному дереву, если нет, то добавить),

Далее поочередно добавляем ребра (скажем $ E'$) которые не вошли в оставное дерево. Ищем путь, в останвом дереве между вершинами $E'$, и убираем одно из ребер. Если все работает, возвращаемся к оставному дереву. Сложность тоже вроде $O(N)$.

Общая сложность $O(N)$.

Но я мог и ошибиться.

[worm2]

an2ancan в сообщении #1277305 писал(а):

Ищем путь, в останвом дереве между вершинами $E'$, и убираем одно из ребер. Если все работает, возвращаемся к оставному дереву. Сложность тоже вроде $O(N)$.

Тут даже проще. Во-первых, задача интересуется только операциями включения-выключения, а их тут ровно по 4 штуки на ребро. Но даже если потребовать $O(N)$ для времени работы алгоритма целиком, включая поиски и переборы, то и тут не надо специально искать путь. В дереве каждый узел, кроме источника, будет иметь ровно одно ребро, "ведущее к источнику", остальные будут "отдалять от источника". Это ребро можно для каждого узла пометить при построении остовного дерева. А потом, при тестировании $E'$, выключать ребро, "ведущее к источнику" для любой вершины $E'$.

[nds]

an2ancan в сообщении #1277305 писал(а):

главное описать алгоритм.

Ну, я тогда задачу не понял.
Зачем там условие, что все реле включены?
Если электрическую цепь можно представить в виде дерева (без сросшихся ветвей), то отключение одного реле отключит всю ветку, и это отключенное (или сломанное) реле ни с каким другим не спутаешь.

Или я что пропустил и условия задачи изменились?