ОДУ с дельта-функцией

[Markiyan Hirnyk]

Как решить ОДУ $y''(x)+4y'(x)+4y(x)=\delta''(x+2),$ где $\delta''(x)$ - вторая производная дельта-функции? Это вариация на тему олимпиадной задачи, предложенной на кафедре дифференциальных уравнений МГУ им. М. В. Ломоносова.
Формула $ y \left( x \right) ={\it C_1}{{\rm e}^{-2\,x}}+{\it C_2}{{\rm e}^{-2\,x}}x + \left( x\int \!f \left( x \right) {{\rm e}^{2\,x}}\,{\rm d}x -\int \!xf \left( x \right) {{\rm e}^{2\,x}}\,{\rm d}x \right) { {\rm e}^{-2\,x}} $ для общего решения неоднородного ОДУ $y''(x)+4y'(x)+4y(x)=f(x)$ мне известна. Математика и Мэйпл щелкают это ОДУ как орешек.

[Ms-dos4]

Markiyan Hirnyk
Так ведь

$$\[\int\limits_{ - \infty }^{ + \infty } {{\delta ^{(n)}}(x)\varphi (x)dx} = {( - 1)^n}{\varphi ^{(n)}}(0)\]$$

[Markiyan Hirnyk]

Ms-dos4
Так ведь интегралы в формуле для общего решения ДУ неопределенные.

[Red_Herring]

Markiyan Hirnyk в сообщении #1275410 писал(а):

Так ведь интегралы в формуле для общего решения ДУ неопределенные.

1) Что будет первообразной от $\delta^{(n)}(x)$ ?
2) Теперь $x\delta^{(n)}(x)=-n \dxelta^{(n-1)}(x)$––в силу определения , которое напомнил вам Ms-dos4

[pogulyat_vyshel]

частное решение ищем с помощью преобразования Фурье

[Markiyan Hirnyk]

Red_Herring
1) Первообразная от $\delta^{(n)}(x)= \delta^{(n-1)}(x), \, n>1,$ ну и что дальше?
2) Ничего он мне не напомнил.

-- 16.12.2017, 16:47 --

pogulyat_vyshel
Спасибо за идею. Преобразование Фурье от обобщенной функции является обобщенной функцией, не так ли? Для конкретной функции оно находтся непросто. Пожалуйста, дайте ссылку.

[pogulyat_vyshel]

Иосида Функциональный анализ

[Markiyan Hirnyk]

pogulyat_vyshel в сообщении #1275435 писал(а):

Иосида Функциональный анализ

Пожалуйста, точную ссылку, как принято среди цивилизованных людей. Если процитируете это место, буду признателен. Кстати, задача предлагалась на студенческой олимпиаде в МГУ им. М. В. Ломоносова.

[pogulyat_vyshel]

Markiyan Hirnyk в сообщении #1275436 писал(а):

Пожалуйста, точную ссылку, как принято среди цивилизованных людей

цивилизованные люди обычно бывают способны отыскать в учебнике главу, которая так и называется "преобразование Фурье и дифференциальные уравнения"

Markiyan Hirnyk в сообщении #1275436 писал(а):

Если процитируете это место, буду признателен.

тут местом не ограничишься, тут надо образовываться по полной программе

Markiyan Hirnyk в сообщении #1275436 писал(а):

Кстати, задача предлагалась на студенческой олимпиаде в МГУ им. М. В. Ломоносова.

и что? :)

-- 16.12.2017, 19:16 --

Вот уравнение для Фурье-образа, если не проврался в арифметике:

$$-\xi^2 Y+4i\xi Y+4Y=-\xi^2e^{2i\xi}$$

[Ms-dos4]

Markiyan Hirnyk
Вообще непонятно, кто мешает вам записать определённые интегралы (с переменным верхним пределом) в общем решении (нижние всё равно уходят в константы). Ну и используйте

$$\int\limits_{ - \infty }^x {\varphi (x)\delta (x)dx} = \varphi (0)\theta (x)$$

вместе с

$$\[{x^n}{\delta ^{(n)}}(x) = {( - 1)^n}n!\delta (x)\]$$

Если бы в вашем уравнении было $\[f(x) = \delta ''(x)\]$, то например получается

$$\[y(x) = [{C_1} + {C_2}x + \delta (x) + 4(x - 1)\theta (x)]{e^{ - 2x}}\]$$

.

[Pphantom]

Markiyan Hirnyk в сообщении #1275436 писал(а):

Пожалуйста, точную ссылку, как принято среди цивилизованных людей.

Markiyan Hirnyk, предупреждение за хамство. Подобные пассажи в адрес людей, пытающихся Вам помочь, недопустимы.

[Pphantom]

Тема перемещена из форума «Олимпиадные задачи (М)» в форум «Помогите решить / разобраться (М)»
Причина переноса: тематика.

[Markiyan Hirnyk]

Ms-dos4
Спасибо. Действительно, $y \left( x \right) = C_1{{\rm e}^{-2\,x}}+C_2{{\rm e}^{-2\,x}}x+4\,{\rm Heaviside} \left( x \right) \left( x-1 \right) { {\rm e}^{-2\,x}}+\delta \left( x \right) $ является общим решением ДУ $y''(x)+4 y'(x)+4y(x)=\delta''(x).$
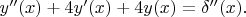
Пожалуйста, дайте ссылку на применяемую вами формулу $x^n\delta^{(n)}(x)=(-1)^n n!\delta(x).$ Не нашел в Вики.

-- 16.12.2017, 18:31 --

Pphantom в сообщении #1275448 писал(а):

Тема перемещена из форума «Олимпиадные задачи (М)» в форум «Помогите решить / разобраться (М)»
Причина переноса: тематика.

См. здесь.

-- 16.12.2017, 18:53 --

pogulyat_vyshel

Внимательно просмотрел гл. VI указанной вами книги
К. Иосида. Функциональный анализ. -Мир.М.:- 1967.-С. 624. Нашел только в $ 2 преобразование Фурье
дельта-функции (но не ее производных) и в $ 6 три примеры решения "операторным методом" ЛОДУ с постоянными
коэффицентами, в правых частях которых - элементарные функции.
Подобная задача предлагалась на студенческой олимпиаде МГУ им. М. В. Ломоносова. Вряд ли студенты
могли пользоваться любыми источниками, кроме собственной головы, при решении задач.
Пожалуйста, объясните, как вами найдена правая часть при преобразовании Фурье обобщенной функции $\delta''(x+2).$

[Red_Herring]

Markiyan Hirnyk
Прочтите свойства преобразования Фурье (книг очень много)
Преобразование Фурье
1) производной
2) сдвинутой функции
3) функции, умноженной на $e^{kx$}
4) функции, умноженной на $x$

Это абсолютно стандартная задача, на стандартные знания, и никоим образом не олимпиадная

Markiyan Hirnyk в сообщении #1275467 писал(а):

Подобная задача предлагалась на студенческой олимпиаде МГУ им. М. В. Ломоносова

Какая конкретно задача, на какой студенческой олимпиаде (для мастематиков или для философов?) и в каком году предлагалась.

Markiyan Hirnyk в сообщении #1275436 писал(а):

Пожалуйста, точную ссылку, как принято среди цивилизованных людей.

[g______d]

Markiyan Hirnyk в сообщении #1275379 писал(а):

Как решить ОДУ $y''(x)+4y'(x)+4y(x)=\delta''(x+2),$ где $\delta''(x)$ - вторая производная дельта-функции?

В каком классе? $\mathcal D’$ или $\mathcal S’$?