Доказать плотность всюду последовательности

в
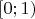
у меня пока не получается,
Поправьте меня если не прав, но это вроде и невозможно. Предварительно две леммы. 1. Число

- иррациональное. 2. Остаток справа после отрезания конечного числа левых цифр от любого иррационального числа является числом иррациональным.
Операция

- отрезает сколько-то левых цифр, оставляя справа все остальные, и для иррационального

остаток будет тоже иррациональным. Т.е. остаются выколоты все рациональные числа. Вах.
В частности, ноль ну никак не получить, ведь тогда число

должно быть целым, значит число

рациональным, но оно же иррационально по условию. Аналогично не получить и числа вида

.
Что однако не является доказательством невозможности получения всех натуральных чисел.