Пытаюсь с помощью ЛЛ-7 разобрать задачу о нагруженном на растяжение стержнем.
Пусть есть цилиндрический стержень, расположенный вдоль оси

. К двум его торцам приложены две силы

и

(соответственно, к площадке с нормалью по оси

и против неё).
В учебнике тензор напряжений вводится так: пусть на произвольный объём тела

действует суммарная сила

где

— объёмная плотность силы, которую можно из-за близкодействия межмолекулярных сил представить поверхностным интегралом вида

где
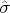
— тензор напряжений. (здесь не нашлось значка для двойного интеграла по замкнутой поверхности
\oiint)
Чтобы задать условия на границе стержня, берём объём

равным самому стержню. Получаем тогда

Противоречий как бы и нет: суммарная сила, действующая на объём стержня, в действительности равна нулю. Но для

я не могу указать определённого значения, так как это слагаемое уничтожается.
Два других уравнения, которые учитывают нулевые компоненты суммарной силы по осям

и

, приводят к

С учётом симметрии тензора два уравнения приходятся на пять неизвестных

,

,

,

и

. Неизвестные

и

вообще из приведённых уравнений выпадают, остаются, стало быть, три неизвестных, но лучше от этого не становится.
В учебнике (другом, не ЛЛ), где эта задача разбирается, пишут: очевидно, что всё, кроме

, равно нулю, а

, где

--- площадь поперечного сечения стержня. Из каких соображений это очевидно, правда, не уточняют.
Вообще, имеем лишь три уравнения для шести компонент тензора
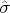
. Где достать ещё три уравнения? Что делать, скажите, пожалуйста?
