Рассеяние на локализованном спине в 1D

[Gickle]

День добрый, такая вот задача попалась. Имеется электрон, который движется слева направо. Имеется обычный дельта-потенциал и в дополнение в точке $x = 0$ находится локализованный спин-$1/2$, взаимодействие с которым модельно описывается дельта-потенциалом следующего вида: $2 J \delta(x) \vec{S} \vec{\sigma}$. Где $\vec{S}$ - спиновый оператор локализованной частицы, а $\vec{\sigma}$ - спиновый оператор электрона (то есть вектор Паули). Электрон имеет волновую функцию вида:

$\Psi(x) = \begin{pmatrix} \psi_{\uparrow}(x) \\ \psi_{\downarrow}(x) \end{pmatrix},$

а локализованный спин:

$\chi = \begin{pmatrix} \chi_{\uparrow} \\ \chi_{\downarrow} \end{pmatrix}$

Собственно, даже дано уравнение Шрёдингера:

$\frac{\hbar^2 k^2}{2 m} \psi_{\alpha} (x) \chi_{\beta} = -\frac{\hbar^2}{2 m} \partial_x^2 \psi_{\alpha} (x) \chi_{\beta} - U \delta(x) \psi_{\alpha} (x) \chi_{\beta} + 2 J \delta(x) (\vec{\sigma} \Psi(x))_{\alpha} (\vec{S} \chi)_{\beta} $

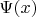
(последнее слагаемое записано как-то коряво в условии, но, думаю, понятно, что имеется в виду, что сначала берётся скалярное произведение от спиновых операторов, а потом уже всем этим винегретом действуем на $\Psi(x)$ и на $\chi$)


"Начальное условие":

$\Psi_{in}(x) = \begin{pmatrix} e^{ikx} \\ 0 \end{pmatrix}$

и

$\chi_{in}= \begin{pmatrix} 0 \\ 1 \end{pmatrix}$

Ну и просится найти коэффициенты прохождения и отражения для спина вниз и вверх.

Методика решения у таких задач всегда одинаковая вроде как. Здесь особенно просто с учётом дельта-потенциала. Слева и справа у нас невозмущённый потенциал, поэтому решением в асимптотике (а в действительности из-за локализованности потенциала - везде) будет волновой пакет. То есть у меня идея искать решения в таком виде:


$\begin{pmatrix} A e^{ikx} \\ B e^{ikx} \end{pmatrix} \otimes \begin{pmatrix} C\\ D \end{pmatrix} $ - справа, поскольку источников у нас справа нет, поэтому волновому пакету с $-k $ взяться неоткуда.

$ \begin{pmatrix} e^{ikx}\\ 0 \end{pmatrix} \otimes \begin{pmatrix} 0\\ 1 \end{pmatrix} + \begin{pmatrix} E e^{-ikx}\\ F e^{-ikx} \end{pmatrix} \otimes \begin{pmatrix} G\\ H \end{pmatrix} $- слева.

Дальнейший алгоритм тогда понятен. Но вот в чём я абсолютно не уверен, так это в асимптотических видах волновых функций. Ну, то есть с частью для электрона всё-более менее ясно - плоские волны и всё тут. А вот с локализованным спином как-то хуже. У меня почему-то плохо укладывается в голове, как представить себе, как это - слева одно, справа - другое. То есть вроде как волновая функция-то у нас, конечно, теперь для двухчастичной системы, но всё равно - разрыв вот этот для локализованного (!) спина, у которого вообще нет координатной зависимости, у меня плохо в голове укладывается. Ну и ещё я как-то не до конца уверен, правильно ли я начальные условия использовал. В смысле законно ли, что я сразу два коэффициента единичками положил (один-то всегда из-за нормировки можно, а тут я сразу два "грохнул").



В общем, буду благодарен, если подтвердите, что ход решения правильный, или укажите, где я неправильно размышляю.

[Munin]

Почему-то словами вы пишете, что "локализованный спин" локализован, а в УШ в последнем слагаемом дельта-функции нет.

Если смотреть на ваше УШ, то "локализованный спин" находится не в точке $x=0,$ а где-то "сбоку", и локализован он только в том смысле, что у него кроме спиновой других степеней свободы нет. А так, он взаимодействует с электроном по всей прямой $Ox$ одинаково.

[Gickle]

Munin в сообщении #1228550 писал(а):

Почему-то словами вы пишете, что "локализованный спин" локализован, а в УШ в последнем слагаемом дельта-функции нет.

Это из-за того, что я очень невнимательный. Извиняюсь, там, конечно, должна быть дельта-функция. Сам, к сожалению, уже поправить не могу.

[Munin]

Тогда напишите в новом сообщении. Ещё можно пожаловаться на своё сообщение модератору, он временно переместит тему в "Карантин", и там вы сможете проделать нужные правки.

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (Ф)» в форум «Карантин»
по следующим причинам:

- временный перенос для правки исходного сообщения.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.

[Pphantom]

Тема перемещена из форума «Карантин» в форум «Помогите решить / разобраться (Ф)»

[Munin]

Gickle в сообщении #1228523 писал(а):

У меня почему-то плохо укладывается в голове, как представить себе, как это - слева одно, справа - другое.

По сути, у вас теперь задача не на одну и не на две комплексные функции $\mathbb{R},$ а на четыре штуки: $\uparrow\uparrow,\uparrow\downarrow,\downarrow\uparrow,\downarrow\downarrow,$ где, например, первая стрелка - электронная, а вторая - локализованной частицы. И в чистом поле они гуляют сами по себе, а в точке $x=0$ переплетаются. Вот и всё.

Gickle в сообщении #1228523 писал(а):

То есть вроде как волновая функция-то у нас, конечно, теперь для двухчастичной системы, но всё равно - разрыв вот этот для локализованного (!) спина, у которого вообще нет координатной зависимости, у меня плохо в голове укладывается.

Это, конечно, диковато, но от непривычки к двухчастичным в.ф. и состояниям. Слышали про такую вещь "нелокальная квантовая запутанность"? Вот это она и есть. Электрон в какой-то точке $x\ne 0,$ и тем не менее запутан (перепутан, зацеплён, сцеплён - entangled) с частицей, сидящей в $x=0.$

Попробуйте порешать задачи... даже не порешать, а просто поглядеть и подумать, над каким-нибудь более простым и интуитивным видом запутанности. Например, пусть у нас два бесспиновых электрона, не взаимодействующих и не тождественных, на одномерной прямой. Тогда их двухчастичное состояние - это функция $\psi(x_1,x_2)$ от двух координат. Как выглядят плоские волны? Как выглядит состояние, которое является волновым пакетом и одного, и второго электрона? Как оно движется по плоскости $(x_1,x_2)$? Возьмём суперпозицию нескольких таких пакетов. Добавим антисимметризацию. Или без антисимметризации, просто потенциал взаимодействия $U(x_1-x_2).$ Пусть у каждого электрона будет ещё и свой потенциал, $U(x_1),U(x_2),$ как они будут сидеть каждый в своей яме (ямах) в разных комбинациях? Ну и всякое такое. Через некоторое время у вас возникнет большее ощущение понимания. А если оно будет пропадать - вернитесь к простым примерам. (Этот пример - хорош ещё и для того, чтобы потом подумать над атомом гелия, или над молекулой $\mathrm{H_2}.$)

[Gickle]

Munin
Большое спасибо. Я на самом деле где-то так себе это всё и представлял, но хотелось надёжного мнения со стороны услышать. :)

Цитата:

Слышали про такую вещь "нелокальная квантовая запутанность"?

К своему стыду, у меня даже семинар в этом семестре по квантовой запутанности есть, так что меня, по идее, эта задача вообще не должна была смущать. Но таки неопытность сыграла роль свою.