Может быть я не прав (тогда поясните, пожалуйста, почему), но по-моему утверждение
Мы не можем вычислить в явном виде

, т.к.

-- аксиальный вектор,-- и мы не знаем, как такие векторы преобразуются
является троллингом. Кто эти "мы", которые не знают, как преобразуются аксиальные векторы?
Аксиальный вектор

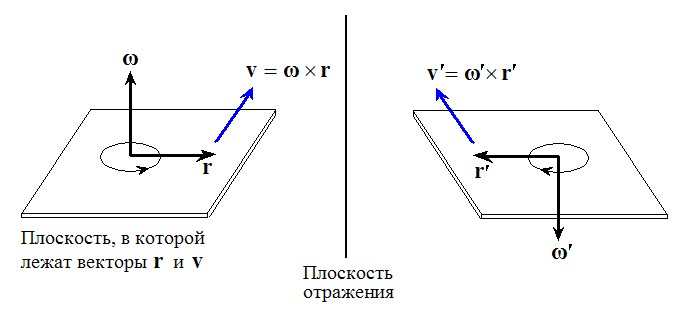
преобразуется, наглядно говоря, как ось вращения колеса. Если при преобразовании получается колесо, вращающееся с той же по величине угловой скоростью, но в противоположную сторону, по сравнению с исходным, значит

Если в ту же сторону, то

Эти и все прочие варианты следуют из реального наблюдения колёс, вращающихся вокруг всяких разных осей, а их описание на языке математических моделей - из построений типа отражений точек относительно плоскостей и поворотов радиус-векторов точек, и сравнением результата в модели с наблюдениями колёс.
Добавлю, что векторы всех типов - геометрические объекты, с которыми можно (а на стадии обучения этому
необходимо научиться) иметь дело в бескоординатной форме, как с объектами на чертежах. Это важно потому, что в физических явлениях координат нет, а сами явления, которым в моделях удаётся сопоставить векторы, - есть.
После того, как геометрическая картина выяснена, да, удобно для дальнейших расчётов ввести так или иначе направленные декартовы орты, разложить по ним все векторы, и тем самым перейти от черчения к алгебре. Тогда преобразование компонент любого истинного вектора

при повороте или отражении в общем виде описывается формулами линейного преобразования с коэффициентами

зависящими от выбора оси поворота или плоскости отражения:

(по дважды повторяющемуся индексу здесь и далее подразумевается суммирование).
При этом закон преобразования любого псевдовектора

имеет вид:

,
где

- определитель матрицы с элементами

причём, доказывается, что

в случае поворота и

в случае отражения - вот тот "дополнительный минус" в законе преобразования псевдовектора, о котором говорилось мной выше.
(Кстати, аналогично определяется и закон преобразования псевдотензора любого ранга: он записывается так же как закон преобразование истинного тензора того же ранга, дополненный множителем

На этом языке формула векторного произведения имеет вид:

,
где

- единичный совершенно антисимметричный (к перестановкам любых двух индексов)
псевдотензор 3-го ранга; проверяется, что он оказывается инвариантным и к поворотам и к отражениям:

Отсюда следует, что:

.
Можно ли утверждать, что это то же самое, что

Да, потому что именно такой результат дают и непосредственные наблюдения, т.е. геометрические построения с отражёнными векторами

и

Вот пример при частном выборе плоскости отражения: