Методика определения делимости чисел

[Iosif1]

PAV писал(а):

. Возьмите хотя бы двух- или трех-значное число и покажите, как с помощью Вашей методики проверить его на простоту. Тогда может быть что-то станет понятно.

На основании использования мод 6 все, названные нами « труднораспознаваемыми», составные числа распределяются по четырем таблицам. (Аналогично системе координат) Первый, второй, третий, четвертый квадранты. Простые числа в таблицах не фиксируются, так как их номера не могут быть выражены в виде, например : $N_1 =6xy+x+y$.
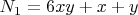
Номер числа – это частное от деления числа (за вычетом единицы, или после ее прибавления) на 6. Если за вычетом единицы, рассматриваемое число относится к первой числовой ветви, если после прибавления - ко второй числовой ветви. В результате определения номера числа отбрасывается, как не нужные для анализа рассматриваемого числа, восемь вариантов расчета. (Расчетных страниц.) ( Всего расчетных страниц 16). На основании четности номера числа, определяется также возможные варианты четности координат, так как коэффициент 6 позволяет это сделать. Предположим, мы взяли для анализа число 8077.
$N={8077-1}/6=1346$
Теперь мы можем утверждать, что в рассматриваемом случае могут иметь место один из двух вариантов четности координат: либо: чет; чет; либо: нечет нечет. Предполагаем, например, что это второй вариант четности координат. Теперь определяем минимальное, возможное значение суммы координат, ( разность координат определяется для чисел другой числовой ветви). Минимальное положительное значение равно 2 (получаемый остаток при делении номера числа на 6. (Для первой таблицы остаток определяется со знаком $+$ . Составляем числовой ряд возможных значений искомой величины:
2…..8…..14…..20…..26…..32… (1)
Строим аналогично числовой ряд величин при использовании мод 4: Получаем:
0…4…8…12…16…20…24…28… (2)


На основании алгоритма перевода, рассчитанного для принятого варианта четности по данной таблице, осуществляем обратный перевод значений 2 числового ряда в значения, первого числового ряда. (Это стало возможным, так как корни квадратного уравнения составленного по мод 6 находятся в корреляционной зависимости с координатами числа, (корнями квадратного уравнения), составленного по мод 4). Корреляционная зависимость между координатами позволяет определять алгоритм перевода и для величин, в которых фигурируют координаты. Для каждой таблицы все строго детерминировано.)
0…..2…..4,666…..7,333…..10…..12,666…..15,333…..18…..20.666…..23.333…..26…(3)
На основании сравнения значений первого и третьего числовых рядов строим числовой ряд целочисленных значений , общих для этих числовых рядов. (с интервалом 24)
2…..26…..50…..74 (нецелочисленные значения нас не интересуют).
И числовой ряд Дискриминантов, соответствующих использованию модуля 6, который в данном случае рассчитывается по формуле:
$D={(x+y)^2/4 - (N-(x+y))/6}$
-222…..-52…..408…..1156…..2192…..3516…..5128…..7028……
Определяем числовой ряд значений величин ${x+y}$, (5) с расчетом начальной величины, и далее с интервалом, равным 4. (Интервал тоже определен расчетным путем, этот интервал является максимально допустимый, не обеспечивающий пропуска требуемого расчета.. (Таким образом строим первый столбец). Увеличивая значение начальной величины 5 на шаг, равный 24, строим второй столбец аналогичных значений, после нового увеличения начального значения величины 5 на шаг, равный 24, строим третий столбец. Если считать эту операцию трудно затратной можно обойтись и двумя столбцами, третий используется для проверки точности проведенных расчетов. Каждый столбец значений 5 участвует в определении разности величин ${D- a^2}$.(6)
Получаем соответственно три столбца таких значений. Теперь определяем построчно разность между соседними значениями последних столбцов. Эта разность для каждой строки постоянная. (Если постоянная: расчеты правильные). Теперь делим значение 6 первого столбца на разность, соответствующую этой строке. Получаем столбец частных. Частные могут быть и дробными и целочисленными. Целочисленное частное показывает, сколько просчетов необходимо произвести, если использовать принятый шаг между просчетами, чтобы найти целочисленные корни квадратного уравнения. Но это если повезет. Величина строк до появления целочисленного значения в столбце может быть самая различная. Нас поразила эта закономерность. Получается, что между разностями Дискриминант и квадратов сумм координат и разницей между этими разностями, при определенных условиях, наличествует линейная зависимость. Мы даже осмелились назвать обнаруженный прием альтернативным методом решения квадратных уравнений. Это нам уже показалось вполне заслуживающим внимания. Но трудоемкость поиска еще не была побеждена. Сделав же аналогичные расчеты для альтернативного решения квадратных уравнений, составленных с использование мод 4., была получена возможность сопоставления результирующих частных по первому и второму вариантам. И оказалось, что если число принадлежит предполагаемой таблице, получаемые частные по первому и второму вариантам для каждого расчета идентичны. Это и обеспечивает незначительные затраты времени при проведении расчетов по определению простоты чисел. А если тождественность частных не обеспечивается, то значит, рассматриваемое число не принадлежит данной таблице. Поэтому, чтобы проверить простое или нет рассматриваемое число, достаточно провести расчеты по четырем расчетным вариантам. Для нахождение же сомножителей требуется продолжать расчеты искомых частных. Нами замечено, что при этом, как нам кажется, для определения зоны расчетов могут использоваться сходимости результатов. Но об этом говорить окончательно рано, хотя нам кажется, что дальше много разных тропинок. Даже приходят на память строки: «Там на неведомых дорожках следы невиданных зверей!» Но я остановился, итак не могу никому объяснить пройденный путь. По моим логическим оценкам временные затраты незначительные. Может быть, факторизация числа более трудно затратная операция. Не могу оценить, не знаю, как делятся числа, выраженные в 256 счислении. Если аналогично числам, выраженным в десятичном счислении, то эта задача для полученного алгоритма вполне по силам и без плазменного компьютера. Iosif1

[PAV]

Еще раз большая просьба: прочитывайте свои же посты после публикации на предмет ошибок в формулах. В одном из своих предыдущих постов Вы хотели написать $10_{10}$, а получилось $10_10$. Понимаете разницу (наведите курсор мыши на формулу, чтобы увидеть, как она набрана).

В самом последнем посте опять возникают непарные скобки, а также минус в формуле для $D$ написан неверно.

Прочитывайте свои сообщения (можно еще перед оптравкой, с помощью кнопки "Предварительный просмотр") и исправляйте ошибки, иначе снова придется применять административные меры.

[Iosif1]

PAV писал(а):

В самом последнем посте опять возникают непарные скобки, а также минус в формуле для написан неверно.

Право не пойму, где знак минуса написан не верно. Я уже научился править. А вот рассеянность мне так и не удается победить. Понимаю, что извиняться бессмысленно.

[PAV]

Iosif1 писал(а):

Предположим, мы взяли для анализа число 8077.
$N={8071-1/6}=1346$

который в данном случае рассчитывается по формуле:
$D={(x+y)^2/4 – (N-(x+y)/6}$

В первой формуле лучше все-таки поставить скобки. Там же неверное число. На вторую посмотрите сами. И со скобками там не все верно.

[Iosif1]

PAV писал(а):

В первой формуле лучше все-таки поставить скобки. Там же неверное число. На вторую посмотрите сами. И со скобками там не все верно.

Благодарен за замеченные опечатки.Данный пост дан для оценки затрат времени, и врядли может быть использован как точный вариант расчета. Однако, обещаю, впредь, быть более внимательным, стараясь не делать ошибок по невнимательности. Iosif1

[Razard]

Пытался разобраться в предложенном алгоритме...

1. (8071 - 1) / 6 = 1345, а не 1346. Или здесь "закопана свинья"?
2. Приведите, пожалуйста, пример для пары чисел, описав конкретно по пунктам каждое действие. Например, для 8059 и 8083.

Если метод теоретически работоспособен - напишу программу для произвольных чисел.

[Iosif1]

Razard писал(а):

. Или здесь "закопана свинья"?

Нет, никакой свиньи, уверяю Вас, кроме того, что сейчас год свиньи. Я списал число 8071 с другого анализа. Я, право, любитель делать ошибки. Понимаю, что это не прибавляет авторитета. Чем Вам не нравится число, рассмотренное мною в примере здесь от 15 декабря 2006 года. Принципиального различия при анализе ваших и моего числа нет. Я внес исправление. Давайте поэтапно, как будто мы беседуем. Можно и по моему, и по вашим числам. Где требуется разъяснения и почему. Так, мне кажется, горазда эффективней. Давайте, в личной переписке:
[e-mail]. Таким способом задавать вопросы, наверно, сподручнее. Итак, $N={(8083-1)}/6=1347$.
Строим числовой ряд возможных корректирующих величин по модулю 6. Этот числовой ряд начинается с остатка, получаемого при делении номера числа, в данном варианте 1347 на 6. Остаток в данном варианте равен 3. Поэтому получаем числовой ряд:
3,9,15, 21....
На основании проведенных расчетов можно утверждать, что одна, из названных нами, координат числа четная а другая нечетная. Это определяет проверочные варианты расчетов, которые необходимо проводить при анализе данного числа.
Данное число может принадлежать (в названной нами системе координат) к одному из двух квадрантов (таблиц). При этом в каждом из квадрантов может иметь место два варианта: или координата $x$ - четная; или координата $y$ - четная. Таким образом нами определены четыре расчетных варианта, которыми следует пользоваться при проверке рассматриваемого числа на простоту (максимальное количество таких вариантов, ведь и при первом варианте расчета может оказаться, что число не простое, если оно принадлежит выбранной таблице). Для каждого такого варианта нами составлены программы посредством использования таблиц Эксель (всего 16). А вот разводка, ввод числа нам не повиновались. Можно ли сделать такую программу, чтобы вводимые числа для проверки увеличивались последовательно, с увеличением предыдущего числа, например на 24? После окончания проверки каждого числа выдавая информацию о том, простое оно или нет, или выражая его в виде произведения. Iosif1

[Iosif1]

Удивлён, думал, что эта тема закрыта.
Эта очередная попытка, обратить внимание, математической общественности на работу, которую правильней, по моему мнению, можно назвать:
«Детерминированный метод факторизации чисел, основанный на существующих расчётных закономерностях, с использованием mod 6 и mod 4» .


Во-первых, потому, что такого решения факторизации чисел не было.

Во-вторых, потому, что методика содержит возможности усовершенствования, обеспечивающие сокращения временных затрат.
(анализируя расчётные закономерности при увеличении интервалов просчёта).

В третьих, потому, что методика, априори, до его факторизации, позволяет определять простоту числа, с незначительными временными затратами.

В четвёртых, потому, что методика позволяет решать квадратные уравнения посредством линейных зависимостей.
Показать работу, для меня, оказалось тяжелей, чем решить задачу.
Попробовал заинтересовать работой посетителей Хабрахабра, именно, на основании четвёртого утверждения.

Это ссылка на Хабрахабр.

https://habrahabr.ru/post/301094/

В отзывах, всё что угодно, только нет понимания.
Написал туда же статью: "Математика Пупкина",
ссылка

https://sohabr.net/habr/post/323700/.

И, что тут началось. И в результате меня лишили возможности общения.
Правда, следует сказать, что и до этого, надежд было не много.
Продвижение без программы, адаптированной к большим числам, не возможно.
Да, и в одиночку, для меня, не подъёмно.
А хочется, всё же, найти понимание.

[Brukvalub]

Iosif1 в сообщении #1206394 писал(а):

И, что тут началось. И в результате меня лишили возможности общения.

Горячо и всесторонне одобряю принятое там решение! Прежде, чем делать "открытия" нужно хотя бы познакомиться с тем, что сделано в данной области до "открывателя". Тогда не придется некропостить в надежде обратить на себя внимание.

[Iosif1]

Brukvalub в сообщении #1206410 писал(а):

Iosif1 в сообщении #1206394 писал(а):

И, что тут началось. И в результате меня лишили возможности общения.

Горячо и всесторонне одобряю принятое там решение! Прежде, чем делать "открытия" нужно хотя бы познакомиться с тем, что сделано в данной области до "открывателя". Тогда не придется некропостить в надежде обратить на себя внимание.

Вы утверждаете, что всё это известно.
Позвольте ссылку.
Заранее благодарен.

[Brukvalub]

Iosif1 в сообщении #1206417 писал(а):

Вы утверждаете, что всё это известно.

Не нужно перевирать мои слова, приписывая мне всякий бред.
Ваш "алгоритм" просто никому не нужен, поскольку давно придуманы весьма эффективные алгоритмы проверки чисел на простоту. Вы не потрудились с ними ознакомиться, а просто нагородили что-то там, и требуете, чтобы с вами "общались видные математики". Оно им надо? Вы не смогли изложить свой "алгоритм" на общепринятом для описания алгоритмов языке, не доказали, что он всегда корректно работает, не привели оценок его эффективности ни по одному из стандартных параметров, не сравнили его эффективность с уже известными алгоритмами, а просто вывалили кучу сумбура и затребовали "общения с великими умами".
Чтобы с ними общаться, мало быть обычным фриком...

[Iosif1]

Brukvalub в [url=http:// dxdy.ru/post1206420.html#p1206420]сообщении #1206420[/url] писал(а):

Чтобы с ними общаться, мало быть обычным фриком...

Не знаю, что такое фрик, или кто такой - посмотрю.
А Вам, как заслуженному участнику, не интересно?
Я бы, и на своём уровне развития, поинтересовался, и как это решена задача, которой тысячи лет.
Что касается великих умов в нынешнем времени, по данной теме, они мне не известны.
Я бы с удовольствием к ним обратился.

[Dmitriy40]

Iosif1 в сообщении #1206394 писал(а):

Продвижение без программы, адаптированной к большим числам, не возможно.

Программа PARI/GP (есть тема на этом форуме про начало работы с ней) вполне себе адаптирована к большим числам и не так уж сложна, состоит буквально из одного запускаемого файла, помощь по функциям и синтаксису встроена в саму программу. Если не требовать сверхбольшой скорости вычислений, то для начала она вполне достаточна.

((не)желание автора)

Почитав реакцию автора на хабре, понимаю что никакой помощи он не просит, а упорно настаивает чтобы поняли его текст, без всяких правок, дополнений, переформулировок и оформления в виде алгоритма (последовательности действий/шагов). Вот есть откровение - и в таком виде его и надобно использовать. А ничему другому автора не учили и соответственно ничего он улучшать не желает. Печально.

[Brukvalub]

Iosif1 в сообщении #1206428 писал(а):

Что касается великих умов в нынешнем времени, по данной теме, они мне не известны. Я бы с удовольствием к ним обратился.

Чтобы к ним обратиться, нужно, для начала, выполнить непосильные для вашего уровня требования:

Brukvalub в сообщении #1206420 писал(а):

Вы не смогли изложить свой "алгоритм" на общепринятом для описания алгоритмов языке, не доказали, что он всегда корректно работает, не привели оценок его эффективности ни по одному из стандартных параметров, не сравнили его эффективность с уже известными алгоритмами, а просто вывалили кучу сумбура и затребовали "общения с великими умами".

СтОит начать с вопроса к себе: а зачем я нужен великим умам? Что я такого ценного и великого открыл и, вообще, мог ли открыть, если я даже не способен оформить свое "открытие" должным образом?

[Iosif1]

Dmitriy40 в сообщении #1206429 писал(а):

Если не требовать сверхбольшой скорости вычислений, то для начала она вполне достаточна.

А Вы не смогли бы мне помочь, сделать это, как соавтор?
Честно, нуждаюсь в соавторе.
Арифметические приёмы в методике доступные для понимания.
Я постараюсь быть полезным.
По мере сил.

-- Вт апр 04, 2017 13:39:08 --

Brukvalub в сообщении #1206433 писал(а):

Чтобы к ним обратиться, нужно, для начала, выполнить непосильные для вашего уровня требования:

Это сказано абсолютно правильно.
Поэтому мне и нужен соавтор.

Brukvalub в сообщении #1206433 писал(а):

СтОит начать с вопроса к себе: а зачем я нужен великим умам? Что я такого ценного и великого открыл и, вообще, мог ли открыть, если я даже не способен оформить свое "открытие" должным образом?

На этот вопрос, я давно ответил утвердительно. Стоит.
И в этом нет ничего от фрика,
Фрик старается эпатировать, а я по другому не умею.