Всем доброго утра. Имеется одно задание, с которым мучаюсь уже пятый день, исписал 11 (кроме шуток) листов А4, чувствую, что сам не справлюсь. Алгоритм решения в общих чертах понимаю, путаюсь в процессе решения, на всякий случай умозаключения тоже опишу (может, в них ошибка). Задание:
вычислить поток векторного поля через полную поверхность пирамиды в направлении внешней нормали к её поверхности непосредственно и применив теорему Остроградского-Гаусса. Пирамида образована некой плоскостью и координатными плоскостями. Сама плоскость:  , векторное поле:
, векторное поле: .
.Собственно, задания тут 2: 1. Найти
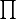
методом Остроградского и (2) "вручную". Просьба не язвить над ошибками, кроме форума и сухих книг подсказать мне некому.
1. Начал с Остроградского-Гаусса:

Сразу
вопрос #1: это верное решение? Значит, если искать поток непосредственно, то его составляющие либо будут равны нулю, либо будут компенсировать друг друга (ну или и то, и другое)?
2. Ищу непосредственно:
Суммарный поток равен сумме потоков, проходящих через каждую сторону пирамиды:

Сначала найдём поток через сторону AOB. Учитывая, что

, получим:

Найдём поток через сторону BOC: учитывая, что

, получим:

Далее - поток через AOC: учитывая, что

, получаем:
 Вопрос 2
Вопрос 2: это верно?
Поток через сторону ABC самый сложный:

,

Вопрос 3: это тоже верно?
Собственно, я понимаю, что дальше надо вычислять эти два поверхностных интеграла, но начинается жуткая путаница с самим интегрированием. Пытаюсь свести к двойному и не понимаю, как именно заменить

на

(в прямом смысле слова не понимаю, смотрю в книгу, вижу фигу), пытаюсь свести его к поверхностному 2-го рода (около 5 листов занимался только этим) и путаюсь окончательно. Попытки решения могу выложить, если надо.
Где у меня ошибка? С какого именно момента я начинаю топтаться на одном месте? Буду очень благодарен тому, кто понятными (и, желательно, не язвительными) словами объяснит, где у меня начинаются ошибки, и было бы ещё лучше, если бы кто-нибудь подсказал первые шаги по взятию получившихся интегралов.
Чуть не забыл - график и его проекции с вычисленными уравнениями прямых (для определения пределов интегрирования):
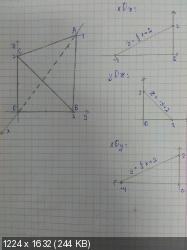
Заранее большое спасибо.