На форуме то и дело возникают темы, в которых один или несколько участников не понимают смысла импликации и её связи со связкой "если... то" в повседневной речи.
Предлагаю своё объяснение импликации для таких участников.
----------
Обычно в математических рассуждениях встречаются импликации вида

, где

и

- высказывания, зависящие от некоторой переменной

(или нескольких переменных).
Например, высказывание "Если натуральное число

делится на

, то оно делится и на

" можно записать в виде

, где

"Число

делится на

",

"Число

делится на

".
Приведённая импликация является истинным утверждением для всех

. Это значит, в соответствии с таблицей истинности импликации, что если

истинно, то

может быть только истинным, а если

ложно,

может быть каким угодно. Смотрим:
- при

,

ложно,

ложно

импликация

истинна;
- при

,

ложно,

истинно

импликация

истинна;
- при

,

ложно,

ложно

импликация

истинна;
- при
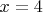
,

истинно,

истинно

импликация

истинна;
- при

,

ложно,

ложно

импликация

истинна;
- при

,

ложно,

истинно

импликация

истинна;
- при

,

ложно,

ложно

импликация

истинна;
- при

,

истинно,

истинно

импликация

истинна;
- при

,

ложно,

ложно

импликация

истинна;
...
Мы видим, что при всех

импликация истинна. Она была бы ложной для некоторого

, если бы для этого

утверждение

было истинным, а утверждение

в то же самое время - ложным. Но таких строк здесь у нас нет. Импликация истинна при всех

.
----------
В тех случаях, когда значений

в импликации

может быть бесконечно много (как в приведённом примере), особенно видна связь импликации со связкой "если... то" в повседневной речи и даже с причинно-следственной связью.
В самом деле, просматривая таблицу выше, рано или поздно мы уверимся:
это неспроста, что каждому истинному

соответствует обязательно истинное

. Если бы эти

и

были никак не связаны между собой, наверняка для какого-то

случайно получилось бы так, что

истинно, а

ложно. Но этого нет. Это даёт нам уверенность, что каким-то образом истинность

обеспечивает истинность

; другими словами, из

следует

.
Это и есть импликация. Сказать "

верно для всех

" - это то же самое, что сказать "Если

верно, то и

верно", или сказать "Из

вытекает

".
----------
Вот, скажем, импликация "Если натуральное число

делится на

, то оно не делится на

" уже не является верной при всех

.
Пусть

"Число

делится на

",

"Число

не делится на

".
Тогда:
- при

,

ложно,

истинно

импликация

истинна;
- при

,

ложно,

ложно

импликация

истинна;
- при

,

истинно,

истинно

импликация

истинна;
- при
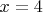
,

ложно,

ложно

импликация

истинна;
- при

,

ложно,

истинно

импликация

истинна;
- при

,

истинно,

ложно

импликация
 ложна
ложна.
Мы видим, что при

истинность импликации нарушается.
То есть, из

вовсе не вытекает

; нельзя сказать, что "Если

верно, то и

верно".
----------
Когда мы говорим "если... то" в повседневной речи, чаще всего при желании это тоже можно записать в виде импликации.
Например: "Если упадёшь с десятого этажа, то умрёшь".
Это утверждение можно записать в виде

,

,
где

- множество людей (как живых так и мёртвых),

"Человек

упал с десятого этажа",

"Человек

умер".
Можно составить список всех людей, когда-либо живших на Земле - наподобие таблиц в примерах выше.
Большинство из этих людей никогда не падали с десятого этажа - для них

будет ложно. При этом для некоторых из них

будет истинно (они умерли, хотя и не по причине падения с десятого этажа - например, от старости, или попав под машину, или будучи затоптаны мамонтом, или упав не с десятого, а с двенадцатого этажа), а для некоторых

будет ложно (они ещё живы). Во всех этих случаях импликация

будет истинной (потому что

ложно, а из лжи может следовать что угодно).
Но также в нашем списке будут присутствовать люди, когда-либо падавшие с десятого этажа, и для них

будет истинно.
Для всех этих людей мы проверим истинность

. Если

для всех этих людей истинно (все они умерли), то для них для всех будет верна импликация

. Тем самым, будет верно и наше изначальное утверждение

,

. И так как множество

очень большое, такое совпадение (что для всех

импликация оказалась истинной) наведёт нас на мысль, что совпадение это не случайное, и между падением с десятого этажа и смертью, видимо, имеется причинно-следственная связь.
Но, быть может, мы найдём в нашем списке такого человека

, для которого

верно (он упал с десятого этажа), но

ложно (он жив). Что ж, тогда для такого

импликация

будет ложной, и наше утверждение

,

тоже окажется ложным. Этот счастливчик

будет контрпримером к нашему утверждению.
----------
Я подчеркну ещё раз, что когда у нас есть импликация

,

, верная для всех

из достаточно широкого множества

, мы можем подозревать причинно-следственную связь между

и

. Импликация ни в коем случае не доказывает эту причинно-следственную связь, но делает очень правдоподобным предположение о её присутствии - ну не могло же случайно так получиться, что для всех-всех-всех

из огромного множества

утверждение

оказалось верным. И ни разу не получилось так, что

истинно, а

ложно.
Если же у нас есть "одиночная" импликация

, то делать на её основе какие-то предположения о логическом следовании или причинно-следственной связи будет опрометчиво.
Отсюда и недоумения по поводу верных импликаций типа "Если

, то я Папа Римский" или "Если

, то Москва - столица России".
-- 19.01.2017, 12:46 --(Оффтоп)
"Если упадёшь с десятого этажа, то умрёшь"
Сразу уточню кое-что, чтобы никто не придрался.
Если эти слова обращены к
конкретному человеку ("если
ты упадёшь с десятого этажа, то умрёшь"), то они не эквивалентны утверждению

,

, которое относится ко всем людям, жившим до сих пор.
Но если они произносятся в смысле "каждый, кто падает с десятого этажа, умирает" - то вполне даже эквивалентны.
Прошу тех, кто будет здесь писать, не прицепляться к подобным незначительным моментам.