Помогите разобраться с задачкой. Пусть
![$m[f]$ $m[f]$](https://dxdy-01.korotkov.co.uk/f/4/b/e/4be6128029c51160337ea28c242e334782.png)
- нижняя грань функции на промежутке

. Доказать что если функции

и
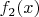
определены на

, то
![$m[f_1+f_2] \geqslant m[f_1]+m[f_2]$ $m[f_1+f_2] \geqslant m[f_1]+m[f_2]$](https://dxdy-02.korotkov.co.uk/f/1/a/c/1ac044bdd327bd648381c2fbfca3e4ea82.png)
.
Понятно что

![$m[f_1(x)] \leqslant f_1(x)$ $m[f_1(x)] \leqslant f_1(x)$](https://dxdy-02.korotkov.co.uk/f/5/a/6/5a61b2c77e5c7552abb49ecf80261e4082.png)
по определению нижней грани, тоже самое для функции
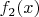
тогда сложив оба неравенства имеем:
![$m[f_1(x)]+m[f_2(x)] \leqslant f_1(x) + f_2(x)$ $m[f_1(x)]+m[f_2(x)] \leqslant f_1(x) + f_2(x)$](https://dxdy-01.korotkov.co.uk/f/8/4/3/843e47d4af9fa79f40ad0b532daa3ec882.png)
дальше не понимаю как. Если обозначить

то нужно показать что нижняя грань множества значений функции

больше либо равна сумме нижних граней составной функции т.е.
![$m[f_1(x)]+m[f_2(x)] \leqslant m[f_3(x)]$ $m[f_1(x)]+m[f_2(x)] \leqslant m[f_3(x)]$](https://dxdy-03.korotkov.co.uk/f/a/c/5/ac5bb592c777acef42227cfcacd4381082.png)
, но на основе чего делать такие выводы не понимаю, подскажите пожалуйста.