Экспериментальное определение плотности распределения

[Gickle]

Доброго времени суток, возник следующий вопрос. Предположим, решили мы побросать "монетку" (несимметричную, чтоб хоть чуть-чуть интереснее было), задавшись вопросом "а какова вероятность того, что из $N$ бросков в $k$ случаях выпадет решка?" Ожидаем, разумеется, биномиальное распределение получить. А как вот это по уму делается? Ну, то есть понятно, что можно, скажем, провести серию из $K$ экспериментов по $N$ бросков, потом сделать гистограмму, аппроксимировать и всё в таком духе. Но это, по-моему, какой-то жутко прямолинейный и глупый способ. Как это делают умные люди? Поверхностный поиск в интернете ничего не дал, как ни странно.

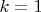
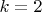
P.S. Из предположений было что-то вроде сразу зафиксировать границы для своей экспериментальной функции плотности распределения, а потом в каждом эксперименте просто ждать, пока не выпадет очередное $k$ в этих пределах. То есть сначала узнать, сколько бросков для $k = 1$ надо, потом - для $k = 2$ и т.п. Ну и в каждом случае провести небольшую серию, по которой усреднять потом. Только мне кажется, что это ровно настолько же эффективный метод.

[arseniiv]

Gickle в сообщении #1168488 писал(а):

Как это делают умные люди?

Умные люди проверяют гипотезу/ы о распределении/ях и оценивают параметры (уже при условии, что распределение известно).

См. учебник матстатистики — например, этот.

[Gickle]

arseniiv
Это уже когда "результаты эксперимента" имеются на руках. А вот получить необходимые данные более разумным методом, чем "$K$ серий по $N$ бросков", можно как-нибудь?

[arseniiv]

Я лучше вам отсебятину не буду говорить, но вот зачем распределять броски по сериям заранее независимо от того, что потом с результатами бросков будет делаться, непонятно. Может, критерию, по которому мы будем определять, какую из гипотез принимать, никакие серии не нужны.

[Gickle]

arseniiv
Ну, в случае с монеткой мне это как-то естсественным казалось: разбить на серии бросков, тогда пространство событий будет состоять из элементов типа "выпало $N$ штук решек в серии".