Условие:
Плотность жидкости

. В начальный момент она заполняет вертикальный участок длины

в тонкой L-образной трубке. Найдите, как зависит от времени высота уровня жидкости. Найдите распределение давления в момент, когда высота столба уменьшится наполовину.
Ответ:


в вертикальной части трубки,

в горизонтальной части трубки.
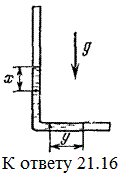
Пробовал записать уравнение Бернулли, но посмотрев ответ понял, что не все так просто. Не понимаю откуда этот косинус. Ещё вводит в ступор то, что проекция скорости(производная

) выходит отрицательная.