Здравствуйте, помогите разобраться с некоторыми вопросами
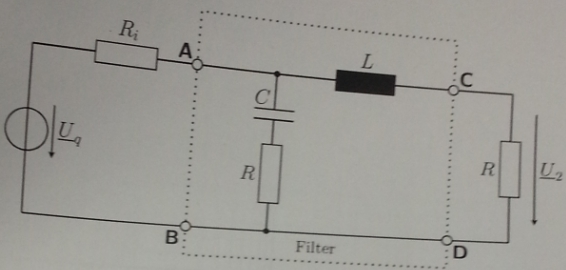
Дана схема выше и по ней вопросы
а) Какие значения принимает

при

и

. Обоснуйте свой ответ (без длинного решения)
Может я что-то не понимаю, но напряжение

это напряжение на резисторе справа, а он от частоты вообще не зависит же, значит оба значения ноль. Или я что-то не вижу?
-- 13.08.2016, 01:31 --b) Надо найти общее сопротивление

на клеммах AB и привести его к виду

Ну тут

параллельно

и вроде все понятно, правда при разделении на действительную и мнимую часть

выглядит громоздко
c) Для специального случая

принимает

реальное значение. Посчитайте его. Зависит ли полученное значение от

?
Т.е. как я понимаю из задания, после того, как

заменяем на

у нас мнимая часть в

уходит в ноль и остается только действительная. И в действительной части комплексного числа есть

, значит она зависит от

.
d) Задайте для специального случая

комплексное соотношение напряжений

. Используйте результат полученный в
c)Если я правильно вижу, то

?
Где

это параллельное соединение

и

и исходя из задания выше у меня там только действительная часть
Немного сумбурно написано, но надеюсь вопросы понятны и мои ответы тоже и вы сможете их оценить, спасибо)