Иными словами, какое наименьшее значение может принимать модуль разности куба нечётного составного числа и факториала натурального числа?
Частичное решение, чтобы строго завершить, у меня немножко культуры и/или сообразительности не хватает:
1. Для наименьшего нечетного составного числа

имеем

2. Факториал четен, а куб нечетного числа нечетен, следовательно, меньшие значения модуля разности могут быть только

, если существуют
3. Из них,

легко отсеиваются, т.к. кубы дают остатки

по модулю

, а факториал будет делиться на

, начиная с

4. Остается проверить наличие решений вида

Здесь могу предложить только нестрогое рассуждение: в разложении

всегда будут вылезать "очень большие" простые множители и, поэтому, "

никогда не догонит

" в силу чего решения, меньшего найденного в п.1 значения

, не существует.
(Оффтоп)
-- 29.06.2016, 02:17 --всегда будут вылезать "очень большие" простые множители
Что, кстати, не факт. Мне показалось, что наибольший простой множитель будет не менее
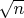
, однако, иногда это не так, например, для
 -- 29.06.2016, 02:20 --
-- 29.06.2016, 02:20 --Хм, впрочем, с учетом кратности множителя,

. А тогда еще "плохой" пример:
