Кажется, можно и прямо в лоб:
1. в критических точках

, где

. У уравнения

не более двух корней, поскольку заменой

оно приводится к виду

, - пересечение прямой и всюду вогнутой функции.
2. значит, достаточно проверить точки

; при

и
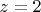
неравенство выполняется строго, остается отыскать локальные экстремумы функции

, т.е. корни

при

. Их два, меньший из них

дает локальный минимум и равенство, а больший - корень

, лежащий между

и

, - локальный максимум, не требующий проверки.