Задача про энтропию

[1_23Kb]

Здравствуйте! У меня возникла проблема с задачей по теории вероятностей:
В испытании с тремя исходами, имеющими вероятность p,q,r, энтропия H$\leqslant1$. Доказать, что max(p,q,r)$\geqslant1/2$
Нашел формулу, что энтропия для дсв равна

$$H(\xi)=-\sum\limits_{i}^{}p_i\log_2p_i$$

, то есть зависит только от вероятностей. Но я не понимаю, как её применить к задаче, как именно доказать. Получил пока только следующее:

$$-p\log_2p-q\log_2q-r\log_2r\leqslant1$$

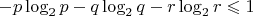
Буду признателен за помощь.

[provincialka]

Может, от противного? Предположите, что все вероятности меньше $1/2$. Кстати, могут ли $p,q,r$ быть произвольными?

И поправьте формулы, а то попадете в Карантин. Например, ставьте перед названием функции бакслэш. Сравните $log_2$ и $\log_2$

[Lia]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы);
- отсутствуют собственные содержательные попытки решения задач(и).

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.