Как влияет орбитальное движение спутника на его собственное вращение?
Допустим спутник движется по круговой орбите и вращается вокруг своей оси, направленной под углом к оси орбитального движения:

- радиус орбиты,

- угловая скорость орбитального движения,
Как учесть орбитальное движение в уравнениях Эйлера:




Иллюстрация взята из источника: С.М. Тарг. Краткий курс теоретической механики.
Вместо

в кинематические уравнения Эйлера следует подставить величину

.
Уравнения движения я вывел с помощью уравнений Лагранжа второго рода.
Кинетическая энергия тела на орбите равна:

,
Выкладки слишком объемны, чтобы здесь их приводить, но я проделал их держа в руках второй том Тиссерана, с. 374.
Однако Тиссеран отталкивается от непривычной формы записи кинематических уравнений Эйлера:



И в итоге получает следующую тройку уравнений Эйлера:



Я же взял привычные кинематические уравнения с "правильной" расстановкой знаков, и получил почти такие же уравнения, за исключением смены знаков в первых двух в правой части перед синусом и косинусом:



Теперь потенциал.
В обозначениях приведенного рисунка связь системы координат связанной с осями инерции и орбитальной системы координат устанавливается матрицей поворота, она же матрица направляющих косинусов

:

Если текущий радиус-вектор спутника направлен по оси

, то нам потребуется первая строчка направляющих косинусов.
Потенциал спутникового приближения довольно легко записывается через направляющие косинусы, и немного сложнее через углы Эйлера...

Вернемся к кинетической энергии.
Абсолютная угловая скорость равна



Теперь кинетическая энергия запишется:
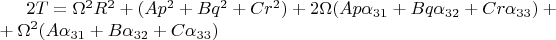
Можно доказать (но я пока не могу), что существует интеграл вращательного движения и устойчивому движению соответствует минимум приведенного потенциала:

когда главные оси инерции располагаются : А - по радиус вектору, В - по касательной, С- перпендикулярно плоскости орбиты.
А это значит, что орбитальное движение стремится поставить самую короткую ось инерции Земли С перпендикулярно плоскости орбиты, что и приводит к прецессии оси вращения Земли...