Общее решение:
Очевидно, на край доски ставить нельзя.
Посчитаем максимум для чёрных клеток. Разобьём внутренний квадрат
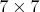
на пять частей (4 красных и одна зелёная на рисунке). В каждой - по пять чёрных клеток.

Ясно, что в красные квадраты по пять шашек на чёрные клетки поставить нельзя, так как тогда центральную никто не бьёт. Предположим, что мы смогли расставить больше двадцати шашек на чёрные. Тогда, по принципу Дирихле, как минимум в одной из пяти частей их больше четырёх. По только что упомянутому, пять их может быть только в зелёном кресте, в красных квадратах тогда по 4 шашки, а всего - 21. Значит, в центра

есть шашка. Её должен бить кто-то из соседей, пусть, без ограничения общности, шашка в клетке 1. Так как все чёрные клетки зелёного креста заполнены шашками, шашку 1 обязана бить центральная, значит в клетке 2 пусто, а тогда шашку 3 (помним, что в красных квадратах по 4 шашки) никто не бьёт, противоречие. То есть на чёрные больше 20 не расставить.
С белыми ещё проще: выделим во внутреннем квадрате 4 области (цветные на рисунке), в каждой из которых по 6 белых клеток, и все белые клетки внутреннего квадрата содержатся в их объединении.

Очевидно, в каждой из областей можно поставить не более пяти шашек на белые клетки, значит всего - не более двадцати.