Функции предполагаются определёнными на измеримом множестве

.
Задача: Пусть

- последовательность простых функций, такая, что
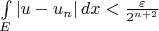
.
Доказать, что

.
Попытки решения: Очевидно, что

(я полагаю

), однако отсюда я получаю неравенство не в ту сторону, в которую мне надо.
Если я пытаюсь работать с модулем, то стандартная техника

не сработает, поскольку я должен получить справа модуль

.
Если делать нестандартно, то возникает величина

, с которой тоже непонятно как бороться. Дайте подсказку, пожалуйста.