Отображение пересечения/разности содержится в пересечении

[math.fi]

Здравствуйте!
Подскажите как показать, что:

$ f(A\cap B) \subset f(A)\cap f(B) $

Вроде бы понятно и очевидно, что в пересечение отображений могут попасть точки из $ f(A \setminus B)$ и $ f(B \setminus A)$, но как это показать?

[Sonic86]

del

[Hasek]

Пусть образы $A$ и $B$ не совпадают. Рассмотрите, например, $x_0 \in f(A) \wedge x_0 \not \in f(B)$.

[math.fi]

Sonic86 в сообщении #1051011 писал(а):

Это ложное утверждение.
Попытайтесь построить тривиальный контрпример - у Вас получится.

Ошибся в выражении Латех'а : вместо команды \setminus вставил обычный \.

[NSKuber]

По определению включений множеств.
Пусть $y\in f(A\cap B)$. Тогда то-то и то-то. Но отсюда следует то-то и то-то, поэтому $y\in f(A)$ и $y\in f(B)$, что и требовалось доказать.

[Someone]

math.fi в сообщении #1051005 писал(а):

Вроде бы понятно и очевидно, что в пересечение отображений могут попасть точки из $ f(A \setminus B)$ и $ f(B \setminus A)$, но как это показать?

Привести пример. А зачем это? Какое отношение точки из $A\setminus B$ или из $B\setminus A$ имеют к образу пересечения?

math.fi в сообщении #1051005 писал(а):

Подскажите как показать, что:

$ f(A\cap B) \subset f(A)\cap f(B) $

По определению: пусть $x\in A\cap B$; тогда…

Извините, подсказывать дальше — это уже практически полное решение, а выкладывать решения учебных задач запрещено правилами.

[math.fi]

Someone в сообщении #1051029 писал(а):

math.fi в сообщении #1051005 писал(а):

Вроде бы понятно и очевидно, что в пересечение отображений могут попасть точки из $ f(A \setminus B)$ и $ f(B \setminus A)$, но как это показать?

Привести пример. А зачем это? Какое отношение точки из $A\setminus B$ или из $B\setminus A$ имеют к образу пересечения?

math.fi в сообщении #1051005 писал(а):

Подскажите как показать, что:

$ f(A\cap B) \subset f(A)\cap f(B) $

По определению: пусть $x\in A\cap B$; тогда…

Извините, подсказывать дальше — это уже практически полное решение, а выкладывать решения учебных задач запрещено правилами.

Очевидно, либо я неправильно понимаю задачу, либо вы.
Начиная доказательство с этого вы докажете, то что и так очевидно. Здесь нужно найти такой $y_0 \in f(A)\cap f(B)$, который $y_0 \not\in f(A\cap B)$. Т.е. что множество справа больше или равно множества слева.
Или я что-то не так понял?

[Brukvalub]

math.fi в сообщении #1051412 писал(а):

я неправильно понимаю задачу

А вот это вы понимаете правильно!

[provincialka]

math.fi в сообщении #1051412 писал(а):

Т.е. что множество справа больше или равно множества слева.

Хм... Если "равно", то почему же $y_0$ не принадлежит?

[math.fi]

Brukvalub в сообщении #1051413 писал(а):

math.fi в сообщении #1051412 писал(а):

я неправильно понимаю задачу

А вот это вы понимаете правильно!

Очень содержательно! Может быть, если вы поняли, что я понимаю неправильно, то распишите здесь то, что, как вы считаете, поняли правильно?

[provincialka]

math.fi
Нет, нельзя расписывать, вам же сказали про полное решение учебной задачи!
А правильно -- так: что надо доказать? Что одно множество есть подмножество другого. А что это означает?

На самом деле доказательство, как вы и сказали, тривиально!

[math.fi]

provincialka в сообщении #1051418 писал(а):

math.fi
Нет, нельзя расписывать, вам же сказали про полное решение учебной задачи!
А правильно -- так: что надо доказать? Что одно множество есть подмножество другого. А что это означает?

На самом деле доказательство, как вы и сказали, тривиально!

Мне кажется, что если вы докажете только в одну сторону, то оно будет только наполовину доказано. Нет?
Ведь если вы докажете только то, что одно множество является подмножеством другого, то это, например не исключает, того, что они могут быть равны всегда!
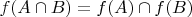
Я вот не верю вам всем. Я утверждаю что $f(A \cap B) = f(A) \cap f(B) $ пока не показано, что могут существовать точки из правой части не принадлежащие левой - можно считать это справедливым.

[Brukvalub]

math.fi в сообщении #1051419 писал(а):

Я вот не верю вам всем.

"В одном переулке
Стояли дома.
В одном из домов
Жил упрямый Фома.

Ни дома, ни в школе,
Нигде, никому -
Не верил
Упрямый Фома
Ничему."
Скоро пойдет вторая страница обсуждений тривиального упражнения! Не много ли чести для подобной мути?

[provincialka]

math.fi в сообщении #1051419 писал(а):

Я утверждаю что $f(A \cap B) = f(A) \cap f(B) $

Это, конечно, не всегда верно. Но если бы было верно, никак не противоречило бы доказываемому вами утверждению!

[math.fi]

Brukvalub в сообщении #1051420 писал(а):

math.fi в сообщении #1051419 писал(а):

Я вот не верю вам всем.

"В одном переулке
Стояли дома.
В одном из домов
Жил упрямый Фома.

Ни дома, ни в школе,
Нигде, никому -
Не верил
Упрямый Фома
Ничему."
Скоро пойдет вторая страница обсуждений тривиального упражнения! Не много ли чести для подобной мути?

Я бы согласился, но на секунду представив, что было бы если бы все всему верили - и дома, и в школе, везед и всем ( особенно в средние века), на меня нашла такая тоска, что я пошел выпить молока с какао.
П.С. Да пожалуй это слишком. Задача у меня никогда не вызывала вопросов, ну вот что-то въелась и не дает покоя. Если уж очень раздражает можно закрывать.