Решается ли парадокс учётом расходимости?
В какие-то моменты на крышке бочки имеется точный нуль поля и, значит, что-то порциями должно поступать внутрь.
Парадокса нет изначально, т.к. является ошибочной фантазия об интерференции "в нуль" на всей крышке бочки.
Думаю, чтобы с этим окончательно разобраться, лучше не останавливаться на частных моделях, а сразу ударить по данной псевдопроблеме из крупнокалиберной пушки - прямо законом сохранения энергии в том его виде, какой известен в электродинамике. Может, кому-то такой подход поначалу покажется сложным, но я постараюсь всё подробно растолковать (хотя это получится не быстро и многословно); во-всяком случае, имхо, это самый прямой и познавательный путь, вот его начало:
Уравнения Максвелла - очень сильная штука; из них математически выводятся не только допустимые в природе конфигурации полей
и
и не только волновое уравнение, управляющее картиной ЭМ-волн, но и важнейшие законы сохранения, в частности: закон сохранения заряда и закон сохранения энергии. Последний давайте разберём подробней (его вывод есть, например, в ЛЛ-2 §31 "Плотность и поток энергии"; у нас речь пойдет о формулах (31,3)-(31,6), но в частном случае и немножко в иных обозначениях).
В случае, когда речь идёт об ЭМ-поле в пустом пространстве (где нет ни источников волн, ни поглощающего вещества), обязательно выполняется вытекающее из ур-й Максвелла вот такое равенство:
![$$-\oint_S \dfrac{c}{4\pi}[ \vec{E} \times \vec{B}]_n \, dS = \dfrac{d}{dt} \int_V \dfrac{E^2+B^2}{8 \pi} \, dV. \qquad (1)$$](https://dxdy-01.korotkov.co.uk/f/8/d/c/8dc6271c3c6c1c36d84ed6febf1a2f8582.png "$$-\oint_S \dfrac{c}{4\pi}[ \vec{E} \times \vec{B}]_n \, dS = \dfrac{d}{dt} \int_V \dfrac{E^2+B^2}{8 \pi} \, dV. \qquad (1)$$")
Разберём, на что и как в нём надо смотреть, если его смысл Вам ещё не известен:
1) Вектор
![$\vec{\Pi}=\frac{c}{4\pi}[\vec{E} \times \vec{B}],$](https://dxdy-02.korotkov.co.uk/f/5/1/d/51d855509661a7cb4ec7d9ae1caff95c82.png "$\vec{\Pi}=\frac{c}{4\pi}[\vec{E} \times \vec{B}],$")
называемый вектором Пойнтинга, в случае ЭМ-волны указывает направление движения волны. Его величина пропорциональна произведению величин магнитного и электрического полей:
Из решения конкретных задач выясняется, что по физ. смыслу
есть плотность потока энергии ЭМ-поля; компоненты этого вектора имеют размерность
2) Важно, что поля являются функциями координат точек пространтва. Поэтому и вектор Пойнтинга, раз он вычисляется через поля, будет свой в каждой точке пространства, т.е. это
локальное понятие. Там и тогда, где поля обращаются в ноль (или делаются маленькими по величине), вектор
тоже обращается в ноль (или становится маленьким).
3) Выражение под знаком интеграла в левой стороне равенства (1) мы можем записать короче:
Это есть произведение элемента площади
и проекции вектора Пойнтинга
на направление нормали данного элемента площади. Знак интеграла с кружком означает суммирование таких локальных вкладов от всей замкнутой поверхности
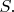
Подразумевается, что любую замкнутую поверхность
мы можем представить себе "склеенной" из элементов площади
, и у каждого элемента площади есть свой вектор нормали (перпендикуляр к площадке), направленный
наружу от данной замкнутой поверхности.
Значит, в каждом месте поверхности величина
если она положительная, равна количеству энергии, выходящей за время
из объёма, ограниченного замкнутой поверхностью
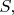
наружу через данный локальный участок поверхности. Если же энергия
в каком-то участке отрицательная (т.е. вектор Пойнтинга в данном месте "смотрит" внутрь поверхности, и поэтому его проекция на нормаль отрицательна), то, значит, через данный элемент поверхности
энергия втекает в объём, ограниченный рассматриваемой замкнутой поверхностью. Таким образом, без множителя
величина
есть мощность потока энергии (c размерностью
, идущего через элемент площади
по отношению к направлению "наружу"; а интеграл по всей поверхности даёт суммарную мощность, проходящую через всю поверхность
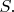
4) В равенстве (1) интеграл по поверхности присутствует с минусом, т.е. левая сторона равенства (1) есть мощность энергообмена через поверхность
по отношению к направлению "внутрь". Другими словами, если на большей части поверхности вектор Пойнтинга смотрит внутрь, то интеграл окажется отрицательным, а взятый с минусом он даст положительную величину: это мощность, поступающая в объём
через ограничивающую его поверхность
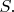
Равенство (1) говорит нам, что этой мощности равна производная по времени от интегральной величины в правой стороне (так что указанная производная тоже положительна). Если же вектор Пойнтинга по большей части поверхности смотрит наружу, то "мощность, поступающая внутрь" и производная в правой стороне (1) будут отрицательными.
интерпретируется как объёмная плотность ЭМ-энергии. Это локальная величина, определяемая значениями полей в данном месте пространства. Тогда
есть количество энергии в данном элементе объёма
а интеграл в правой стороне (1)
будучи суммой локальных вкладов
по объёму
даёт количество ЭМ-энергии
во всём объёме
Значит, равенство (1) можно записать в краткой форме так:
и передать его смысл словами так:
мощность, поступающая внутрь объёма через его поверхность, равна скорости изменения энергии, заключённой в этом объёме.Теперь уже очевидно, это просто-напросто одна из формулировок закона сохранения энергии, и в словесной форме она выглядит даже тривиальной. Математическая форма (2) более содержательна, т.к. в ней более-менее явно определён количественный смысл слов. А лучше всего подробная запись (1): она позволяет детально анализировать связь между всеми существенными локальными понятиями.
И самое главное: равенство (1) справедливо для объёмов
, ограниченных поверхностями
любой формы и любого размера. Для анализа картины ЭМ-поля мы можем выбирать воображаемые объёмы
в виде бочек, бутылок, коробок, менять их размер, поворачивать их так и эдак, отслеживая локальное распределение плотности потока энергии (вектора Пойнтинга) на том или ином участке ограничивающей поверхности
Чтобы лучше уяснить, что даёт полезного нашему пониманию равенство (1), мы ниже рассмотим два тренировочных примера. А в третьем примере покончим с вопросом об интерференции лучей.
а поле второго луча описывать "синусоидой в противофазе",
то в суммарном поле автоматически возникают и минимумы, 
и 
, т.е. функции вида
- скорость света, 
- величина волнового вектора 
указывающего направление распространения волны, 
- произвольная начальная фаза) как раз являются одной из разновидностей решений волнового уравнения; сумма любого количества таких решений (с произвольными постоянными амплитудами, произвольными фазами 
) тоже есть решение волнового уравнения. 
) устроены как раз так же. Значит, наша модель двух лучей будет полностью верна при условии постоянства амплитуд 
обеих синусоид, т.е. - верна для неограниченно широких лучей, называемых "плоскими волнами". Короче говоря, самые правильные картинки из приведённых выше это те, в которых световое поле заполняет всё пространство рисунка: 
с П-образной амплитудой 
скачком обращающейся в ноль вне луча. Такие функции, увы, не удовлетворяют волновому уравнению и поэтому не могут служить точным описанием реальных пучков света. К приведённым выше картинкам с лучами конечной ширины надо относиться так: они дают нам некое представление об интерференции в области перекрытия лучей, но только вдали от краёв этих модельных лучей; картина вдали от краев лучей тем ближе к правде, чем больше ширина лучей превышает длину волны 
Вблизи же краев, а тем паче при малой ширине этих модельных лучей такие картинки неверны, поскольку в них не учтено дифракционное уширение лучей.
Но на самом деле это не так! Приближение геометрической оптики работает тем хуже, чем меньше размер отверстия; на самом деле световое поле за экраном складывается из волн с разными по направлению волновыми векторами, т.е. свет за экраном идёт не только в прежнем направлении, но и в разные стороны. А если размер отверстия мал в сравнении с длиной волны, то пучок света за экраном вообще "размывается" по углу почти равномерно: маленькое отверстие светит во все стороны, а не узким пучком. (Численное моделирование тут будет делом более хлопотным, нежели приведённый раньше простой подсчет синусов; предъявить результат сию минуту не обещаю... :)
Чтобы смотреть интерференцию двух гауссовских пучков, их тоже следует вычислять на одной и той же сетке точек, записав две формулы: для пучка, распространяющегося вдоль 
и для пучка, распространяющегося под заданным углом к оси 
Вроде, особой сложности в этом деле нету; надо только превозмочь лень да избежать ляпов из-за невнимательности)).
)
и 
очень велики по сравнению с их значениями вдали от луча. Поэтому для наглядности здесь можно рассуждать приближённо без заметной потери точности, - можно представлять себе, что луч входит в нашу воображаемую бочку через небольшой участок левой крышки с площадью 
и выходит через участок 
правой крышки, а дифракционным распространением поля через боковую поверхность бочки пренебрегать. (Впрочем, всё это не обязательно; равенство (1) работает во всех случаях.)
. Так, если излучение монохроматическое, т.е. оно имеет определённую частоту, 
то усредняем за период колебания: 
Если же в спектре излучения есть разные частоты, то усредняем за время 
в нашей бочке c течением времени не накапливается и не убывает монотонно (а может только с какой-то большой частотой то возрастать, то убывать - в соответствии с поступлением в бочку и уходом из бочки очередной пучности ЭМ-поля). Поэтому в стационарном случае усреднённая по времени скорость изменения энергии в бочке равна нулю. Схематичная картинка:
воображаемой внутренней перегородкой произвольной формы. Для левого объёма, 
эта перегородка будет играть роль правой части его замкнутой ограничивающей поверхности 
а для объёма 
эта перегородка будет левой частью его ограничивающей поверхности 
(причём, для 
). Дык вот: все предыдущие выводы будут верны и для каждого из объёмов 
и 
