Преобразование "прямая-точка", расширенное до "линия-линия"

[Rybalko]

Я придумал таковое (http://www.neizvestniy-geniy.ru/persona ... 11111.html).

А из подобного нашел только «обобщённое преобразование Хафа» (патент 1962 г. Поля Хафа).
Однако мне сообщали, что близкое преобразование было опубликовано еще в 30-х годах и вроде бы в СССР.
Может, кто-то подскажет, где его искать, чтобы я не публиковал уже известное...

Спасибо за ответы!

Вот пояснение...


Задача оперирования линиями—траекториями возникает по ассоциации с треками в ядерной физике.

Определение 1. Будем называть маршрутами любые линии в двухмерном пространстве, которые имеют конечную первую производную всюду в открытом промежутке за исключением, быть может, множества без конечных точек сгущения.
Определение 2. Будем называть особыми точками маршрута исключительные точки из определения 1.
Итак, для удобства оперирования маршрутами введем еще одно двумерное пространство, в котором каждый маршрут будет иметь свой образ, простой для важного класса маршрутов — прямых. В частности, если бы образы прямых были точками, это позволило бы легко находить расстояние между линиями этого класса.
Построение пространства образов маршрутов и начнем с прямолинейных маршрутов, исключая такие, которые параллельны оси ординат. Каждая такая прямая определяется двумя параметрами (а для прямых, параллельных оси ординат, это как раз и неверно). Возьмем за основу асимметричную формулу прямой: $v = ku + b$.
Определение 3. Фундаментом отображения типа "линия — линия" будем называть подмножество его области определения, каждый элемент которого отображается в точку.
В качестве фундамента нашего отображения примем совокупность прямолинейных маршрутов, исключая те, которые параллельны оси ординат. Для этого в пространстве образов маршрутов поставим в соответствие этой прямой (равно как и ее части) точку с координатами (x, y) такими, что $x = b, y = k$ (перестановка координат сделана не случайно: она позволяет получить нетривиальные результаты).
Отображение кривой осуществляем на основе приближения ее ломанной, каждый прямолинейный отрезок которой отображается в соответствующую ему точку. Если у кривой существует первая производная, то при неограниченном уменьшении максимума длины отрезков ломанной, последняя будет стремиться к нашей кривой. При этом направления отрезков будут стремиться к направлению касательной, так что интуитивно оправдано считать образом кривой предел образов ломанных, ее приближающих. Тогда координаты точки кривой в мире образов маршрутов (x, y) будут выражаться через значения координат и производной кривой в исходной плоскости (u, v):

$$x = v – uv', y = v'.$$

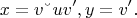
В общем случае, когда кривая состоит из дискретного множества участков, на которых существует первая производная, формулы остаются в силе, но в точках излома (разрывы первой производной) отдельно рассматриваются левосторонняя и правосторонняя производные. Это, очевидно, породит разрыв образа и по ординате и по абсциссе; правда, в нулевой абсциссе разрыва маршрута по абсциссе никогда не будет, поскольку абсцисса соответствующей точки образа всегда равна ординате маршрута.

Если кривая задана в параметрической форме, координаты точки кривой в пространстве образов маршрутов (x, y) будут выражаться следующим образом: $x = (φ(t) / ψ(t))' ψ²(t) / φ'(t), y = ψ'(t) / φ'(t)$, где [/math]$φ(t) и ψ(t)$[/math] — параметрические задания переменных u и v соответственно.

[Lia]

Уточните заглавный вопрос, пожалуйста. Не вполне ясно, о чем речь.

[Rybalko]

Это преобразования, которые переводят линию в другую линию. И естественно, что должен быть контент, цель, приложения, а не произвол. Разумеется, нетривиальные. Таково упомянутое «обобщённое преобразование Хафа».

[Hasek]

Любая изометрия переводит линию в линию.

[arseniiv]

Rybalko в сообщении #1024620 писал(а):

переводят линию в другую линию

Прямые линии или любые кривые? Иначе вообще любой гомеоморфизм на себя сойдёт. С прямыми — аффинные преобразования (обратимые).

[Rybalko]

Я же написал: с нетривиальным развитием, т. е. содержательными свойствами.
А вообще-то меня интересует построение такого преобразования на фундаменте преобразования типа "прямая линия - точка". (Я наработал кое-что в этом направлении, послал в журнал, а оттуда ответили, что подобное преобразование уже было опубликовано... Этот ответ у меня, к сожалению, затерялся.)

[arseniiv]

Rybalko в сообщении #1024633 писал(а):

Я же написал: с нетривиальным развитием, т. е. содержательными свойствами.

Странное словоупотребление, так что не удивляйтесь, что вас не поняли. (А то контент, цель приложения, да ещё и нетривиальные (и почему-то это должно разуметься).) Если линии имелись в виду прямые, то в аффинных преобразованиях (конечных пространств) разворачиваться особо некуда. Если кривые, то, наоборот, разнообразие просто не позволяет взять и выбрать что-то единственно интересное. Например,

$$(x,y,z)\mapsto(x,e^{ax}(y\cos\omega x-z\sin\omega x),e^{-ax}(y\sin\omega x+z\cos\omega x).$$

По мне, весьма нетривиально, а контент так вообще прелесть.

[Rybalko]

arseniiv в сообщении #1024648 писал(а):

Если линии имелись в виду прямые

...
Имеется в виду преобразование, которое прямую переводит в точку, а что становится с непрямыми -- предмет исследования. Там могут быть и обобщения, и расширения, и количественные характеристики, и построение пространства с необычными свойствами...

[svv]

Когда Вы давали название теме и когда писали вот это

Rybalko в сообщении #1024620 писал(а):

Это преобразования, которые переводят линию в другую линию.

— имели ли Вы в виду только прямые линии, или не только? Про точки Вы потом уже заговорили, а мы Вас спрашиваем о том, с чего Вы начали.

По-моему, тема имеет неплохие, заслуженные шансы уехать в Карантин.

[arseniiv]

Rybalko в сообщении #1024652 писал(а):

Имеется в виду преобразование, которое прямую переводит в точку

Одну прямую? И, в любом случае, тогда это опять слишком широкий класс, так как теперь даже и обратимыми ограничиться не удастся.

Rybalko в сообщении #1024652 писал(а):

Там могут быть и обобщения, и расширения

Чего там обобщать? И куда расширять?

Так понимаю, эта тема должна называться «Придумайте за меня интересное мне преобразование, но я не буду вам помогать: угадывайте»?

[Lia]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

Просьба максимально уточнить предмет обсуждения.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.