Вот это нужно обосновать:
отрезок

проходит через центр окружности и соответственно делится пополам точкой

А то Вы более простые места расписываете, а здесь не стали.
Попытаюсь обосновать. Получается такой рисунок:
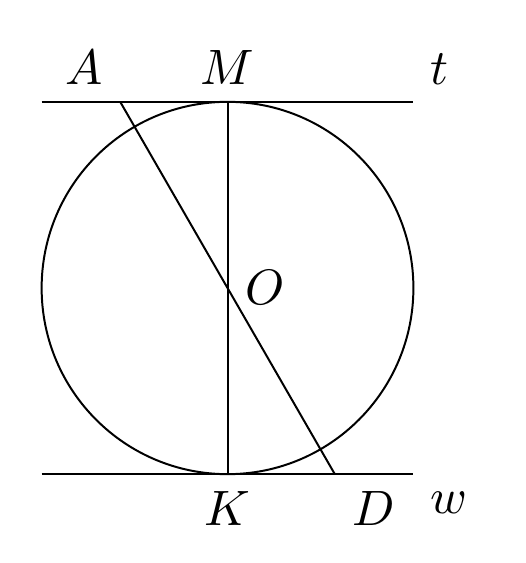
Здесь

и

- параллельные прямые. Между ними вписана окружность, касающееся этих прямых. Центр окружности обозначен точкой

. Таким образом, диаметр окружности

является расстоянием между параллельными прямыми и, поскольку диаметр, делится точкой

на два равных отрезка-радиуса

и

. Возьмём на прямой

точку

и проведём от неё отрезок до точки

и продолжим дальше до пересечения прямой

. Угол

равен углу

и составляет

. Углы

и

- вертикальные, следовательно, равны. Отрезок

равен отрезку

. По второму признаку равенства треугольников (сторона треугольника и два прилежащих угла) треугольник

равен треугольнику

, поскольку

,

и

. Значит, отрезки

и

равны. Следовательно,

делится точкой

пополам.
Дальнейшее всё слишком сложно для такой (относительно) простой задачи, хотя ответ, похоже, правильный. Посмотрите на треугольники

и

. Найдите отсюда выражение для радиуса и подставьте в формулу площади. Найдёте

. Это сделает решение раза в два короче и раза в три проще.
Сейчас попробую. Получается такой рисунок:
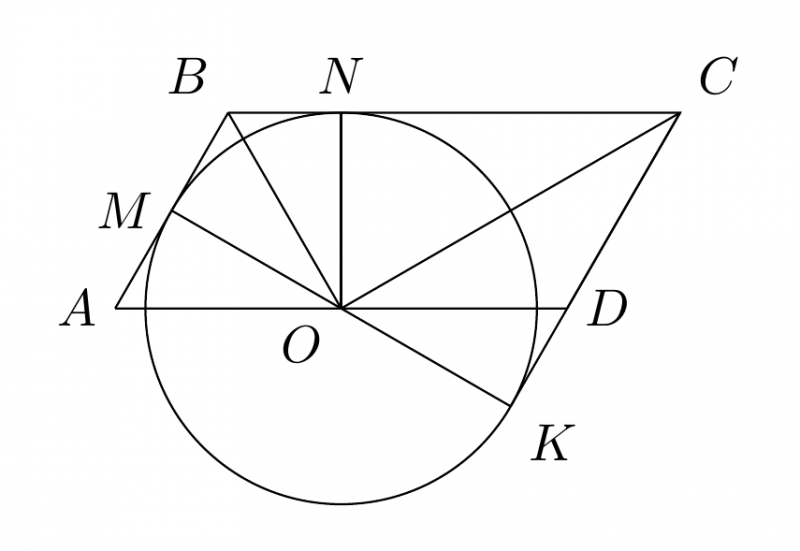
Поскольку мы имеем дело с параллелограммом, то

. Обозначим

, а

. Получаем

. Отрезок

является биссектрисой и делит

пополам, отсюда

, отрезок

является биссектрисой и делит

пополам, отсюда

. Теперь из прямоугольного треуголькника

:

. Из прямоугольного треугольника

:

.

Таким образом


Подставляем в формулу площади трапеции
![$S_{ABCD} = ON \cdot BC \Rightarrow 4 = a \sqrt{3} \cdot 4 a \Rightarrow a = \frac{1}{\sqrt[4]{3}}$ $S_{ABCD} = ON \cdot BC \Rightarrow 4 = a \sqrt{3} \cdot 4 a \Rightarrow a = \frac{1}{\sqrt[4]{3}}$](https://dxdy-04.korotkov.co.uk/f/b/8/b/b8b65d8f6ae6d7835ed8575cc5886fb282.png)
. Сторона
![$BC = 4a \Rightarrow BC = \frac{4}{\sqrt[4]{3}}$ $BC = 4a \Rightarrow BC = \frac{4}{\sqrt[4]{3}}$](https://dxdy-03.korotkov.co.uk/f/2/0/5/20521dbfa785320ef080afc7bcf9f32782.png)
, радиус
![$r = a \sqrt{3} = \sqrt[4]{3}$ $r = a \sqrt{3} = \sqrt[4]{3}$](https://dxdy-02.korotkov.co.uk/f/1/f/2/1f2896e814bbf47cd83ae5d1b6e5f56e82.png)
. Длина отрезка
![$AM = \sqrt{AO^2 - OM^2} = \sqrt{({\frac{2}{\sqrt[4]{3}})}^2 - {(\sqrt[4]{3})}^2} = \frac{1}{\sqrt[4]{3}}$ $AM = \sqrt{AO^2 - OM^2} = \sqrt{({\frac{2}{\sqrt[4]{3}})}^2 - {(\sqrt[4]{3})}^2} = \frac{1}{\sqrt[4]{3}}$](https://dxdy-01.korotkov.co.uk/f/4/5/4/4545a000395ef5210da47314fe8b2bc282.png)
. Длина
![$AB = AM + MB = \frac{1}{\sqrt[4]{3}} + \frac{1}{\sqrt[4]{3}} = \frac{2}{\sqrt[4]{3}}$ $AB = AM + MB = \frac{1}{\sqrt[4]{3}} + \frac{1}{\sqrt[4]{3}} = \frac{2}{\sqrt[4]{3}}$](https://dxdy-04.korotkov.co.uk/f/b/c/6/bc6faf9f282d8bd51a538f73344d509d82.png)
. Да, получилось короче.
Это правда, но слишком долго: синусы тут вообще не при чём, достаточно того, что

из подобия соответствующих прямоугольных треугольников. И сторона

ровно вдвое меньше, чем

, по гораздо более тривиальной причине: просто потому, что удвоенный радиус -- это высота параллелограмма, опущенная на

.
То есть,

. И

. Спасибо
grizzly и
ewert - стало понятно. Но я просто поражаюсь: откуда у вас столько фантазии чтобы подметить эти действительно простые, но крайне незаметные для меня факты?