задаче нахождения минимума

при условии

.
Или минимума

при условии

. Запишем для этой задачи функцию Лагранжа

, где

- двойственная переменная (скаляр). Условие оптимальности - у этой функции существует седловая точка. Допусти нашли оптимальное
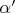
. Тогда седловая точка - это точка минимума по

этой функции Лагранжа для нашего
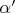
. И эта задача минимизации эквивалента первой задаче, поскольку последний множитель с

можно отбросить. Таким образом понят смысл

, как оптимальной двойственной переменной. И понята равносильность двух задач. Однако у нас пропало

, и получается, что от него ничего не зависит, что странно. Чтобы найти оптимальные

и

, надо записать условие минимума для первой задачи, например. Которое можно записать через субградиенты, например. Ну, или выписывая частные производные и учитывая негладкость.