Выброшенная реактивная масса, в ближней зоне реактивного мотора представляет собой некоторое облако газа.
Нет, так как у нормальных ракет струя вообще сверхзвуковая. Нет никакой "ближней зоны реактивного мотора", не фантазируйте.
Вам совершенно точно не следует считать ракеты - они не имеют отношения к вашему вопросу, к тому же расчёт истечения газа из сопла требует продвинутых знаний из газодинамики.
С Вашего позволения, я попробую разобраться.
Вопрос - какая жесткость у газовой струи из сопла реактивного двигателя если в трюме ракеты на дно упал груз (на пружину).
Мысленно - ударим по воде пробным телом на скорости 1 м/с или 1000 м/с. Или на поршень - налетит струя воды/газа на скорости 1 м/с или 1000 м/с. Положим, что в ракете есть поверхность, на которую бьет струя газа с тепловыми скоростями 1000 м/с. Эта струя летит по вектору тяги. (немного упростим для начала).
Понимаем, что кроме скорости струи есть давление. Рассмотрим статику и динамику. Статика - пример - поплавок медленно погрузился в воду на глубину h. Динамика - прилетел на скорости 1000 м/с и хотел утонуть. На поплавок должна действовать статическая и динамическая сила.
В нашей задаче - "поплавок" - это камера сгорания, в ней есть давление 300 атм и есть "ветер" что передает импульс от горячего газа к ракете через площадь поверхности. Вроде все так..
1. Исходная система и ЛагранжианРассматриваем систему Ракета
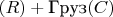
. Струя является внешней средой, взаимодействующей с системой.
Лагранжиан: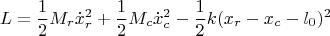
где

— жёсткость пружины,

— её длина в свободном состоянии.
Уравнения Лагранжа: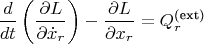
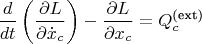 Внешние обобщённые силы:
Внешние обобщённые силы: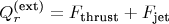
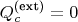 2. Выведем
2. Выведем 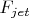 из законов сохраненияРассмотрим Уравнение Эйлера для реактивной струи:
из законов сохраненияРассмотрим Уравнение Эйлера для реактивной струи: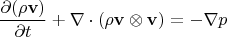
Проинтегрируем по контрольному объёму

, включающему камеру сгорания и ближнюю зону (истечения):
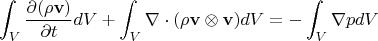
По теореме Остроградского-Гаусса и с учётом, что Сила

Поток импульса через поверхность:
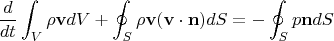
Заметим, что:
В стационарном режиме первый член

0.
При ударе груза возникает нестационарность, и первый член не равен нулю.
Сила реакции на ракету

изменению импульса в контрольном объёме

потоку импульса через его границы.
Предположим, что :Основное изменение импульса происходит в камере сгорания при смещении её задней стенки. Считаем газ в камере "жёсткий амортизатор".
Тут есть вопрос как правильно считать - уточним позже (сопло или камера)3. Вывод рабочей формулыСмещение стенки

за время

создаёт дополнительное давление

.
3.1. Термодинамическая (статическая) составляющая:Из уравнения адиабаты
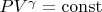
:
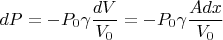 Сила, действующая на стенку:
Сила, действующая на стенку: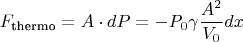
Это квазистатическая жёсткость газа.
3.2. Динамическая (инерционная) составляющая:Смещение стенки со скоростью
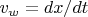
навстречу потоку со скоростью звука

требует изменения импульса набегающих частиц.
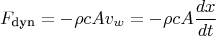
Учитывая, что:
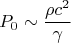
(для идеального газа), получаем:
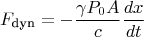
3.3. Итоговая формула для
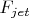
:
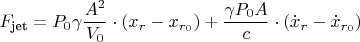
где
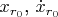
— положение и скорость ракеты до возмущения.
4. Окончательная система уравнений
Подставляя
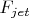
в уравнения Лагранжа, получаем:
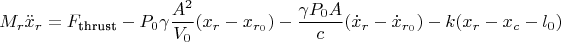
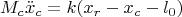
в нашем случае - груз создает удар против хода ракеты, поэтому рабочая формула имеет вид.
Код:
r.a_rocket_x = (Force.Thrust - Force.Friction + Force.Jet_damping)/Rocket.Massa
r.a_cargo_x = Force.Friction / Cargo.Massa
Где:
Force.Thrust - Внешняя сила - тяга мотора
Force.Friction - Сила сжатия пружины (внутренняя)
Force.Jet_damping - Внешняя сила от сопротивления газовой струи.
По примерным оценкам, Force.Jet может быть на уровне 0,001 -0,1 % от Force.Thrust и возможно улучшение.
Заключение - мы искали третью силу (аналог гравитационного якоря). И нашли ее в инерции и жесткости реактивной струи.
Может ли это уменьшить сам Force.Thrust - пока не понятно, но следует хотя бы спросить.