Дано макроскопическое количество радиоактивного вещества, даны интервалы времени во много раз меньше периода полураспада.
Количество распадов за время

зависит только от длины интервала, а не от его положения.

- вероятность

распадов за время


при

,
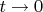

при
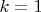
,
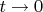

при

,
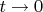
Расписывая

, находят:


Далее пишут

Какой смысл последней записи и что может означать

?
Нужно получить распределение Пуассона для
