В теории чисел совсем не силён, ну вроде что-то получилось. С одной стороны длинно, а с другой стороны:
1) Показано, что двойка тут не при чём и вместо неё можно взять любое положительное число, меньшее

.
2) Найден критерий того, когда неравенство превращается в равенство.
3) Доказано, что в случае неравенства произведений с единичным остатком ровно на 3 больше, чем произведений с остатком, равным другому (заранее данному) фиксированному числу.
Так что решил всё-таки написать своё решение. В общем, поехали!
Надо доказать, что количество троек

, составленных из различных ненулевых элементов

, для которых

не меньше, чем количество аналогичных троек, также составленных из различных ненулевых элементов

, для которых

(умножение, естественно, рассматривается внутри

, ненулевое

фиксировано, в исходной постановке задачи

).
Пусть

--- порождающая мультипликативной группы поля

. Пусть
![$$
X = \{ \langle a,b,c \rangle \in [0,p-2]^3 : a \neq b \mathbin{\&} b \neq c \mathbin{\&} a \neq c \}
$$ $$
X = \{ \langle a,b,c \rangle \in [0,p-2]^3 : a \neq b \mathbin{\&} b \neq c \mathbin{\&} a \neq c \}
$$](https://dxdy-04.korotkov.co.uk/f/3/2/f/32f83ca0342ad97128f0090f163688e482.png)
Ещё одна переформулировка задачи выглядит так: доказать, что

Пусть

таково, что

. Тогда

делится на

и

сравнимо с

по модулю

. Воспринимая компоненты троек, принадлежащих

, как элементы

, получаем ещё одну эквивалентную формулировку исходной задачи: доказать, что

, где
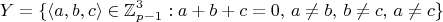
и

Пусть

и

Ясно, что

. Пусть

. Определим отображение

, сопоставляющее каждой тройке

тройку

. Из определений видно, что

инъективно отображает

в

, так что

и

.
Легко видеть, что если

, то

и

, так что в будущем будем считать, что

. Посчитаем количество элементов в

. При задании тройки

из

элемент

можно выбрать произвольно,

задаётся однозначно по

, а

определяется равенством

. Кроме того,

должен отличаться от

и

, так что при выборе

должны учитываться неравенства

и

. Таким образом,

равно количеству элементов

в

, для которых

и

. Ясно, что

равно тому же самому.
Посмотрим, какие элементы

не попадают в образ

. Прямо из определений следует, что

. В случае

отсюда видим, что эта тройка не лежит в образе

тогда и только тогда, когда либо

, либо

. В силу

оба равенства не могут выполняться сразу. Если мы хотим выполнить первое равенство, то

можно выбрать произвольно,

однозначно определится по

, а

найдётся из равенства

. Но

должно отличаться от

и

, так что должны выполняться неравенства

и

. Таким образом, первое равенство можно выбрать столькими способами, сколько существует элементов

в

, для которых

и

. Количество способов, которыми можно удовлетворить второе неравенство, точно такое же. И поскольку в задаче требуется доказать, что количество способов, которыми можно удовлетворить одно из неравенств, не превышает количества элементов в

, то у нас появляется ещё одна переформулировка задачи: доказать, что

Можно даже сделать более сильное утверждение:

отличается от

на количество элементов, равное разности правой и левой частей этого неравенства.
Ну а тут уже всё совсем легко. Если у какого-то из уравнений

,

,

и

есть корни, то их количество равно

в случае, когда

делится на

, и

в противном случае. Уравнение

имеет корень тогда и только тогда, когда имеет корень уравнение

. Действительно, если

корень первого уравнения, то

--- корень второго, а если

--- корень второго, то

~--- корень первого. Аналогично наличие корней у уравнения

равносильно наличию корней у уравнения

. Ну а у уравнения

корни есть всегда и мы доказали всё, что надо.
Под конец ещё заметим, что если

не делится на

, то корни у любого линейного уравнения с коэффициентом

при переменной есть всегда. Сюда же можно приплюсовать случай

, исключённый из рассмотрения ранее, поскольку в этом случае уравнение

имеет корень

.
---------------
Суммируя всё вышесказанное и возвращаясь к исходным обозначениям, получаем, что
1) Если

является кубическим вычетом по модулю

, то в исходной задаче неравенство превращается в равенство
2) Если

не является кубическим вычетом по модулю

, то количество троек с остатком от произведения равным

на

больше, чем количество троек с остатком от произведения, равным

.
Наверное, как-то всё можно было покороче...