Целые корни полинома, состоящего из суммы полиномов

[Anna from Svetl]

Здравствуйте. Такая задача. Имеется полином

$$ \begin{array}{l} -\displaystyle\prod_{i=2}^{l}{(x-2i)}+\dfrac{1}{2\cdot 1!}\displaystyle\prod_{i=3}^{l}{(x-2i)}\displaystyle\prod_{j=2}^{3}{(x-j)}-\dfrac{1}{2^2\cdot 2!}\displaystyle\prod_{i=4}^{l}{(x-2i)}\displaystyle\prod_{j=2}^{5}{(x-j)}-\ldots-\\ -(-1)^{l-3}\dfrac{1}{2^{l-3}\cdot (l-3)!} \displaystyle\prod_{i=l-1}^{l}{(x-2i)}\displaystyle\prod_{j=2}^{2(l-3)+1}{(x-j)}-(-1)^{l-2}\dfrac{1}{2^{l-2}\cdot (l-2)!}\displaystyle\prod_{i=l}^{l}{(x-2i)}\displaystyle\prod_{j=2}^{2(l-2)+1}{(x-j)}-\\ -(-1)^{l-1}\dfrac{1}{2^{l-1}\cdot (l-1)!}\displaystyle\prod_{j=2}^{2(l-1)+1}{(x-j)}. \end{array} $$

Необходимо определить есть ли у него целые положительные корни $k=n+l$, если $l$ может изменяться в диапазоне $\overline{2,n}$.
Сначала я подумала, что поскольку все полиномы, входящие в этот полином, разложены на простые множители, то для того, чтобы $k$ было корнем уравнения, множитель $(x-k)$ должен входить в каждый из суммируемых полиномов, но легко показать, что при заданных условиях это невозможно. А теперь я засомневалась, может ли быть так, что $k$ --- корень полинома, но при этом $(x-k)$ не входит в виде множителя в каждый из полиномов.

[svv]

Конечно, так может быть. Например, полином
$5(x-2)(x-4)-(x-8)(x-10)$
имеет корни $-2$ и $5$, хотя ни $x+2$, ни $x-5$ нигде не было.
Посмотрите, может, есть множители, общие для всех слагаемых.

[Anna from Svetl]

Так вот что-то не получается никак. Не понимаю, куда смотреть. И даже если есть, то что делать дальше.

[svv]

Просто запишу компактно:

$$\sum\limits_{k=0}^{\ell-1}\dfrac{(-1)^{k+1}}{2^k\;k!}\prod\limits_{i=k+2}^{\ell}(x-2i)\prod\limits_{j=2}^{2k+1}(x-j)$$

Произведения, в которых верхний предел индекса меньше нижнего, считаются равными $1$.

[Anna from Svetl]

Тут нет произведений, в которых верхний предел меньше нижнего. И что делать с ними дальше? Скажем, перед первым полиномом стоит коэффициент $(-1)$. Перед всеми остальными --- нет. Как это поможет доказать, что полином не имеет целых корней в заданном диапазоне, или найти такие корни?
P.S. Извините за глупые вопросы, просто раньше с полиномами выше 3-4 степени сталкиваться не приходилось.

[svv]

Anna from Svetl в сообщении #988947 писал(а):

Тут нет произведений, в которых верхний предел меньше нижнего.

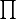
Это только в моей формуле. Я имел в виду вот что. В Вашей формуле в каждом слагаемом стоят два $\prod$, кроме первого и последнего. Если принять это моё соглашение, все слагаемые можно записать единообразно, и вся формула выглядит проще.

В первом слагаемом $k=0$.
Тогда первое произведение будет $\prod\limits_{i=2}^{\ell}(x-2i)$, то есть как у Вас.
Второе произведение будет $\prod\limits_{j=2}^{1}(x-j)$, то есть верхний предел будет меньше нижнего. По соглашению считаем, что оно равно 1 и вообще не пишем его. Получаем Ваше первое слагаемое (с точностью до коэффициента).

В последнем слагаемом $k=\ell-1$. Теперь уже первое произведение будет $\prod\limits_{i=\ell-1+2}^{\ell}(x-2i)$, и его опять считаем единицей. А второе произведение $\prod\limits_{j=2}^{2(\ell-1)+1}(x-j)$ понимаем в обычном смысле.

Во всех остальных слагаемых в обоих произведениях нижний предел $\leqslant$ верхний предел, и их понимаем в обычном смысле.

[Anna from Svetl]

Это я поняла. Зачем это нужно?

[svv]

Для порядка, чтобы легче анализировать полином.

[Anna from Svetl]

Я уже его и так и этак переписывала. И в Maple пыталась эту общую сумму загнать, только Maple выдает какую-то ерунду. Если наложить ограничения, что $l$ целое, то он выдает ошибку "деление на ноль".
Еще пыталась вынести множитель перед произведением, который дает член со старшей степенью, за скобку, и воспользоваться тем, что делители свободного члена могут быть целыми корнями полинома, но я не могу извлечь эти делители из свободного члена.