Прошу помочь решить предел

[Hristell]

Здравствуйте.
Вот этот предел:

$$\lim\limits_{x\to0}^{}\frac{\cos(x+5\pi/2)\tg x}{\arcsin2x^2}$$

Пыталась выражать через формулы приведения, так же пользовалась основным тождеством $\sin^2(x)+\cos^2(x)=1$ , $\tg x=\frac{\sin x}{\cos x}$ и $\arcsin x + \arccos x = \pi/2 $, получилось:

$$\lim\limits_{x\to0}^{}-\frac{1-\cos^2(x)}{\cos x(\pi/2-\arccos2x^2)}$$

и толку нуль, все так же (0/0)

[Lia]

Hristell
Определитесь с аккаунтом. В противном случае будет заблокирован произвольный по моему выбору. Обращаться в ЛС.

-- 01.03.2015, 19:48 --

Hristell
Строгое предупреждение за двойную регистрацию.

Если в ближайшие полчаса в теме не появятся Ваши содержательные попытки решения, она пойдет в Карантин. Это все ни о чем.
И аргумент тангенса напишите, пожалуйста.

[Pphantom]

Hristell, что у Вас является аргументом тангенса в числителе?

Впрочем, если там нет ничего особо экзотического, то формул приведения и того обстоятельства, что $\sin x \sim x$ при $x \to 0$, вполне должно хватить для получения ответа.

[Hristell]

Не углядела, аргумент тангенса является x, исправила.
С формулой приведения можно же прийти только к этому результату:

$$\lim\limits_{x\to0}^{}-\frac{\sin x \tg x}{\arcsin 2x^2}$$

Я не очень понимаю, что мне делать с $\arcsin 2x^2$
Стоит ли его преобразовывать по формуле $\arcsin x + \arccos x = \pi/2$ ?
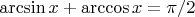
Или есть другой вариант? В интернете встретила вариант с домножением sin... Но не знаю правильно ли, что $\sin(\arcsin 2x^2) = 2x^2$
И правильно ли его использовать в этом случае

[Pphantom]

Hristell в сообщении #984303 писал(а):

С формулой приведения можно же прийти только к этому результату:

А дальше замена на эквивалентную. Причем, заметьте, из $\sin x \sim x$ следует, что и $\arcsin x \sim x$ при $x \to 0$.

[Hristell]

Pphantom, т.е. можно привести к виду:

$$\lim\limits_{x\to0}^{}\frac{x^2}{2x^2}= 1/2$$

?

[Pphantom]

Совершенно верно.

[Hristell]

Охохо, все так не сложно оказывается...
Pphantom, спасибо большое!!

[grizzly]

Hristell
Со знаками будьте поаккуратнее.

[Hristell]

grizzly, точно, минус! Спасибо!