Перенесем

в правую часть, возведем первое уравнение в куб и вычтем второе, получаем:

или

Заметим, что это равенство невозможно, если обе части равны нулю, а поэтому они не равны нулю и

поэтому обязано делить

. При этом остаток от деления многочлена

на

равен 8 и, следовательно,

является делителем этого числа. Таким образом,

или

, а

и

определяются как корни квадратного уравнения

, дискриминант которого обязан быть полным квадратом. Этим условиям удовлетворяет только

,
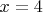
и

. Поэтому
worm2 абсолютно прав.