я видел, я вижу, я умею...
Меняем позицию -- одно из двух: или не умничать, или приводить доказательства. А то потом на поверку, как оказывается, стыда не оберёшься.
Привожу своё решение, развивающее идею касательных. Будем доказывать, что
если два множества имеют хотя бы по одной внутренней точке, а третье имеет больше одной точки, то искомая секущая найдётся. Ниже под касательной понимается касательная к некоторой окружности (про центр и радиус этой окружности в каждом случае будет понятно из контекста).
Пусть, для определённости, множества

и

содержат внутренние точки

и

, соответственно. Пусть

-- ближайшая к

точка чужого множества.
1) Если

, то прямая, проходящая вблизи точки

через

пересечёт все 3 множества (очевидно в силу шевеления касательной).
2) Пусть
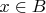
. Используя тот же приём касательных, убеждаемся, что все точки

должны лежать на одной прямой, иначе найдём прямую, пересекающую три множества.
2.1) Рассмотрим теперь точку

. Рассуждая так же, как в п. 1), получаем, что проблемная ситуация возникает только в случае, когда точка

на границе окрестности

принадлежит

. Соединяя

с точками

, убеждаемся (как в п.2), что только для точек, лежащих на касательной к кругу с центром в

, прямая может не пересечь все множества.
3) Из предыдущих рассуждений заключаем, что единственной точкой в

, не дающей нужного решения, может быть только точка пересечения касательных.
Уменьшить третье множество до одной точки невозможно, что показывает пример
gris с конусом.
-- 09.01.2015, 18:38 --В доказательстве есть легко устранимая проблема. Ближайшая точка чужого множества к выбранной внутренней точке может не существовать. Тогда в худшем случае придётся брать нужный супремум в качестве радиуса и рассматривать последовательности "почти"-касательных. Принципиально не испортит, но доказательство удлинится.
-- 09.01.2015, 18:52 --Доказательство
worm2 очевидно проще и приятнее, но оно оставляет лазейку для целой прямой в третьем множестве (если обобщать далее). И я пока не вижу, как избавиться от этой лазейки.