Башней (tower) называется последовательность подгрупп

Башня называется нормальной, если

нормальна в
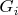
. Если все подгруппы нормальны и абелевы - башня абелева, если нормальны и циклические - циклическая.
Уплотнением (refinement) башни называется башня, которая может быть получена вставкой конечного числа подгрупп в данную башню.
Доказывается утверджение о том, что всякая абелева башня конечной группы допускает циклическое уплотнение.
Если я правильно понимаю, для этого каждая подгруппа в башне должна быть циклической (чтобы в итоге вставили еще несколько подгрупп и все были циклическими).
Но не всякая конечная абелева группа является циклической, например, если взять как множество двоичные последовательности длины

, и как операцию побитовый XOR, получится абелева группа: есть единичный элемент (нули), для каджого элемента есть обратный (он сам), соблюдается ассоциативность и коммутативность. Но эта группа не порождается одним элементом.
В чем я ошибаюсь?