Спасибо, lofar (Христос се роди!

)
Still, I'm not quite shore that this
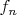
is a Cauchy sequence in a space X (of course, it is sad to be like that, but ..., and isn’t it
![${\|f_n-f_m\|_X}\geqslant {\|f_n-f_m\|_C_{[a,b]}}$ ${\|f_n-f_m\|_X}\geqslant {\|f_n-f_m\|_C_{[a,b]}}$](https://dxdy-04.korotkov.co.uk/f/3/0/1/301ab8f1029cf6cc0415123fb9013aaa82.png)
?). Maybe we can assume something like that, but I think it would be better if there is a defined sequence as a proof of incompletes (caunterexample). Sorry if I sad something incorrect ... is there a link on a similar problem (Functional analysis is new to me, and as an exercise book I use the Задачи в упражнения по функциональному анализу, Треногин В. А., Писаревский В. М., Соболева Т. С, so, is there a link or recommendation for a better exercise book which can be download, or this one is a good choice).
Спасибо.