По оси

в положительном направлении движется с постоянной скоростью

точка

(цель). На плоскости

движется точка

(преследователь) с постоянной скоростью

так, что вектор скорости всегда направлен в точку

. Найти траекторию точки

(кривую погони), если в начальный момент времени

точка

находилась в начале координат, а точка

- на оси

на расстоянии

от цели.
Мои попытки решения: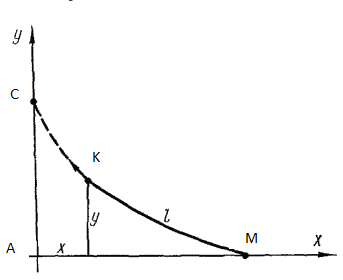
Допустим, что

и

- координаты преследователя в момент времени

. В этот же момент времени цель находится в точке

и она прошла путь

.

- длина дуги MK. Можно вычислить угол наклона касательной в точке

:

.
Длина дуги

Дальше каким-то образом надо связать скорости (

), подставить в

, затем его продифференцировать и решить получившийся дифур. Подскажите, как поступить со скоростями.