А как мне быть с

перед

?
Просто вот я не могу же

просто взять и домножить на

? Немного запутался.
Если Вам дали такую задачу, значит, наверное, была теорема дифференцирования изображения… (или как там она у вас называется).
P.S. Вы не находите, что записи типа

нехорошо выглядят? Я обычно пользуюсь значком "

". Например:
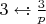
.
Код:
\leftarrow\!\!:
-- Сб дек 06, 2014 20:08:50 --А ещё я встречал значки типа "

" или "

".
Код:
\fallingdotseq \risingdotseq