Вопросик по КТП

[studentmk_32]

Здравствуйте. Помоги, пожалуйста, разобраться.

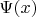
Есть у нас оператор импульса $P = \int\Psi^{\dagger}(\textbf{x})\frac{\hbar}{i}\nabla\Psi(\textbf{x})d^3x$, здесь $\Psi(x)$ - это оператор поля.
Допустим у нас есть бозон в состоянии $|\textbf{r}_1\rangle$. Хотим посчитать $P|\textbf{r}_1\rangle$.

Если вспомнить, что $|\textbf{r}_1\rangle = \Psi^{\dagger}(\textbf{r}_1)|0\rangle$, подставить это и воспользоваться правилами коммутации для операторов поля, то получим: $\int\Psi^{\dagger}(\textbf{x})\frac{\hbar}{i}\nabla\delta(\textbf{x} - \textbf{r}_1)|0\rangle d^3x$. Хорошо, а дальше-то что?

Помоги пожалуйста, никак сообразить не могу.

P.S.
С названием темы промахнулся, по-моему. Вопрос скорее по вторичному квантованию.

[amon]

А Вы что сосчитать-то хотите?

[studentmk_32]

Задача:



Это у меня товарищ проходит какой-то онлайн курс (MIT, по-моему). Что должно получиться в ответе - загадка. Поэтому и спросил у Вас. Может это какая-то стандартная выкладка с красивым результатом. Но в литературе ничего по этому поводу не нашел.

[amon]

Одночастичное состояние выглядит так $|r_1\rangle=\int \varphi(r)\hat{\Psi}^+(r)|0\rangle dr$, аналогично $|r_1,r_2\rangle=\int \varphi(r_1,r_2)\hat{\Psi}^+(r_1)\hat{\Psi}^+(r_2)|0\rangle dr_1dr_2$. Надо подействовать Вашим оператором импульса на эти функции, протащить оператор $\hat{\Psi}$ к вакууму и посмотреть, что получится.

[studentmk_32]

amon в сообщении #933584 писал(а):

Одночастичное состояние выглядит так $|r_1\rangle=\int \varphi(r)\hat{\Psi}^+(r)|0\rangle dr$, аналогично $|r_1,r_2\rangle=\int \varphi(r_1,r_2)\hat{\Psi}^+(r_1)\hat{\Psi}^+(r_2)|0\rangle dr_1dr_2$. Надо подействовать Вашим оператором импульса на эти функции, протащить оператор $\hat{\Psi}$ к вакууму и посмотреть, что получится.

amon

Здесь $\varphi(r)$ - это $\delta(r - r_1)$, так? В этом случае получиться то, что я и написал: $\int\frac{\hbar}{i}\nabla\delta(\textbf{x} - \textbf{r}_1)|x\rangle d^3x$. Наверное, дальше преобразовать нельзя. Зря я маюсь.

P.S.
А запись оператора в таком виде она и в случае фермионов верна? Просто я видел доказательство только для бозонов.

[amon]

studentmk_32 в сообщении #933617 писал(а):

Здесь $\varphi(r)$ - это $\delta(r - r_1)$, так?

Нет, не так. $\varphi(r)$ - это то, что в обычной (не "вторично-квантованной") квантовой механике называют волновой функцией. Т.е. это почти произвольная дважды дифференцируемая функция. Аналогично с $\varphi(r_1,r_2)$. Это - двухчастичная волновая функция.

[type2b]

эту задачу можно решить и без вычислений, из общих соображений. Оператор импульса, как известно -- генератор сдвигов, т.е. $\exp(i\vec{P}\vec{x})|\vec{r}_1,\vec{r}_2,...\rangle=|\vec{r}_1+\vec{x},\vec{r}_2+\vec{x},...\rangle$, откуда $\vec{P}|\vec{r}_1,\vec{r}_2,...\rangle=-i\partial_{\vec{x}}|\vec{r}_1+\vec{x},\vec{r}_2+\vec{x},...\rangle|_{\vec{x}=0}$, что эквивалентно тому, что вы написали. (Только я аш выкинул, и знак еще проверьте.)
Очевидно, это верно и для бозонов, и для фермионов, и для чего угодно при наличии трансляционной инвариантности.

[propagator]

Как вариант: записать оператор импульса через операторы рождения и уничтожения и ними уже действовать на данные состояния.

[amon]

studentmk_32 в сообщении #933617 писал(а):

А запись оператора в таком виде она и в случае фермионов верна?

Да. Только операторы поля для фермионов антикоммутируют.

[studentmk_32]

amon в сообщении #933621 писал(а):

studentmk_32 в сообщении #933617 писал(а):

Здесь $\varphi(r)$ - это $\delta(r - r_1)$, так?

Нет, не так. $\varphi(r)$ - это то, что в обычной (не "вторично-квантованной") квантовой механике называют волновой функцией. Т.е. это почти произвольная дважды дифференцируемая функция. Аналогично с $\varphi(r_1,r_2)$. Это - двухчастичная волновая функция.

Ага, Вы имеете в виду формулу для general one-particle state (я сам учусь по английским учебникам, так что русской терминологии не знаю, извините) $|\psi\rangle = \int |x\rangle \psi(x) dx$? Но мне из задания показалось, что $|r_1\rangle$ - это собственное состояние для оператора координаты. Разве в этом случае $\varphi(r)$ не равно $\delta(r - r_1)$?

[amon]

studentmk_32 в сообщении #933915 писал(а):

$|r_1\rangle$ - это собственное состояние для оператора координаты. Разве в этом случае $\varphi(r)$ не равно $\delta(r - r_1)$?

Для собственного состояния оператора координаты Вы правы.