Определение структурного пучка

[OlgaD]

Помогите разобраться с определением. Чем больше пытаюсь понять, тем сильнее запутываюсь.
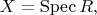
Обозначения следующие: $R$ - коммутативное кольцо с единицей, $X=\operatorname{Spec}R,$ $X_f$ - главное открытое множество (т.е. множество всех простых идеалов $R,$ не содержащих $f$), $R_f$ - локализация по элементу $f.$ Обозначим наш пучок $\mathcal{O}_X$ и его слой в точке $\mathfrak p$ через $R_{\mathfrak p}.$ Определение

Цитата:

Для всякого открытого множества $U\subset X$ положим $\mathcal{O}_X(U)$ равным множеству наборов $\{s_{\mathfrak p}\}\in\prod\limits_{\mathfrak p\in U}R_{\mathfrak p},$ обладающих тем свойством, что существуют покрытие $U$ главными открытыми множествами $X_{f_{\alpha}}$ и элементы $s_{\alpha}\in R_{f_{\alpha}},$ для которых $s_{\mathfrak p}$ совпадает с образом $s_{\alpha}$ в $R_{\mathfrak p},$ как только $\mathfrak p\in X_{f_{\alpha}}.$

Сначала я хотела бы понять: для каждого набора $\{s_{\mathfrak p}\}$ свое покрытие и элементы или они фиксированы?