Собственно, тема весьма давняя и пургаторная в том смысле, что заявления автора ни на чём не основаны. Возможно, были эксперименты с небольшими числами, которые разлагаются на множители за доли секунды методом пробного деления, но такие числа в настоящее время никого не интересуют, а интересуют числа, содержащие сотни цифр в десятичной записи, не говоря уже о поиске рекордных простых чисел, содержащих миллионы цифр.
Однако утверждения о необыкновенной эффективности этого метода вновь
всплыли. Поэтому желательно дать некоторые пояснения.
Сам по себе предлагаемый метод не является новым. Я о нём узнал, ещё будучи младшим школьником (в 1961 году, когда учился в 4-м классе), когда купил в книжном магазине книгу Б. А. Кордемского "Математическая смекалка" (Государственное издательство технико-теоретической литературы, Москва, 1957). Там этот метод называется решетом Сундарама и оформлен в виде двумерной таблицы, строки и столбцы которой являются арифметическими прогрессиями:
Число, расположенное на пересечении строки №

и столбца №

, равно

.
Работает это так. Пусть задано нечётное натуральное число

. Если число

имеется в таблице, то

— составное, если же числа

в таблице нет, то

— простое.
Обоснование очень простое.
Если

— нечётное составное, то есть, существуют такие (нечётные) натуральные

и
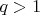
, что

, то числа

,

и

являются натуральными; тогда выполняется равенство

, то есть,

. Следовательно, число

имеется в таблице и расположено на пересечении строки №

и столбца №

.
Наоборот, если число

есть в таблице и расположено на пересечении строки №

и столбца №

, то

и, следовательно, составное.
Совершенно очевидно, что проверка числа на простоту таким методом равносильна частичному разложению на множители и потому не может быть более эффективной, чем поиск делителя. Известно, что поиск делителя — существенно более сложная задача, чем проверка на простоту.
В данной теме предлагается обобщение решета Сундарама:
Для упрощения выражений можно выражать уравнения в виде не чисел, а их номеров, которые определяются как целочисленные частные от деления чисел на выбранные модули, с прибавлением к числам, или вычетом от чисел единицы.
Поэтому каждый номер любого составного числа, не содержащего сомножителей

и

можно выразить вариантами:

; (1)

; (2)
Становится ясно, что если составное число можно, то простое число не может быть так обеспечено одновременно,ибо в таком случае оно становится составным.
Собственно, предлагается для числа

, не делящегося ни на

, ни на

, искать решения четырёх уравнений

и четырёх уравнений

, где

и

(в обоих случаях знак выбирается так, чтобы частное было целым). Непонятно, конечно, зачем так много уравнений. Достаточно найти решение одного из восьми предлагаемых уравнений, чтобы получить разложение числа на два множителя; для доказательства простоты нужно доказать отсутствие решений у одного или двух правильно выбранных уравнений из четырёх первых или из четырёх вторых. Так же, как и для решета Сундарама, задача равносильна поиску делителя и, следовательно, сложнее проверки на простоту.
Правила выбора уравнений.
1)

Если

, то

разлагается либо в произведение

, либо в произведение

. Соответственно, нужно искать решения двух уравнений

и

.
Если

, то

разлагается в произведение

, поэтому достаточно искать решения одного уравнения

(второе уравнение

отличается только обозначениями неизвестных).
Этот вариант решета работает и для чисел, делящихся на

. Правдоподобно, что он равносилен решету Сундарама.
2)

Если

, то

разлагается либо в произведение

, либо в произведение

. Соответственно, нужно искать решения двух уравнений

и

.
Если

, то

разлагается в произведение

, поэтому достаточно искать решения одного уравнения

(второе уравнение

отличается только обозначениями неизвестных).
Очевидный метод поиска решений предлагаемых уравнений состоит в том, чтобы выразить одну неизвестную и подставлять вместо другой последовательные натуральные числа

,

,

,… Например, для уравнения

выражаем

и подставляем вместо

последовательные натуральные числа, начиная с единицы. Останавливаемся, когда получится целое частное, либо частное станет меньше

(для других уравнений условие остановки может быть другим; предлагаемая процедура наверняка не самая эффективная для данных уравнений).
В итоге, я не могу ожидать высокой эффективности обсуждаемого метода по сравнению с другими методами проверки простоты числа, и пока не вижу здесь более эффективного метода поиска делителя, чем "тривиальный" метод пробного деления. Но
Iosif1, разумеется, убеждён, что его метод суперэффективный.