Теорема Уитни

[loshka]

Здравствуйте, помогите пожалуйста понять геометрический смысл теоремы Уитни

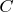
Для любого замкнутого подмножества $ C $ аффинного пространства $A$ на $A$ существует такая бесконечно гладкая функция $F$, что $p$ принадлежит $C$ тогда и только тогда когда $F(p)=0$.


Правильно ли я понимаю, что идея этой теоремы в том что любое замкнутое множество можно представить в виде кривой?

[alcoholist]

loshka в сообщении #899968 писал(а):

Правильно ли я понимаю, что идея этой теоремы в том что любое замкнутое множество можно представить в виде кривой?

Не в виде кривой... ведь $\{(x,y,z)\in\mathbb{R}^3:x^2+y^2+z^2-1=0\}$ не кривая)))
И $\{(x,y,z)\in\mathbb{R}^3:(x^2+y^2+z^2-1)(x^2+y^2+z^2)=0\}$ тем более

[popolznev]

Кривые здесь ни при чём. Смысл теоремы в некотором смысле противоположный: каким бы плохим, страшным и непохожим на кривую ни было замкнутое множество, всё равно оно является множеством уровня некоторой очень хорошей (гладкой) функции.

[loshka]

но разве функция от одной переменной это не есть кривая в n-мерном пространстве??

[alcoholist]

loshka в сообщении #900003 писал(а):

но разве функция от одной переменной это не есть кривая в n-мерном пространстве??

(Оффтоп)

функция не есть кривая, кривая не есть функция

функция откуда куда?

[loshka]

Непрерывное отображение из некоторого отрезка в н-мерное пространство, это есть определение кривой, и в условие теоремы строится отображение зависящее от одного параметра, чистая кривая же?

[alcoholist]

loshka в сообщении #900008 писал(а):

зависящее от одного параметра

$p$ -- это точка в $A$

-- Вт авг 26, 2014 00:32:12 --

$F:A\to\mathbb{R}$

[loshka]

так если отображение непрерывно дифференцируемо, то значит есть и обратное $ F^{-1} : U \to A$ где $U$ некоторый отрезок, а значит и представимо в виде кривой оО

[popolznev]

loshka в сообщении #900015 писал(а):

так если отображение непрерывно дифференцируемо, то значит есть и обратное $ F^{-1} : U \to A$ где $U$ некоторый отрезок, а значит и представимо в виде кривой оО

Пусть функция $F$ тождественно равна нулю. Какая у неё $ F^{-1}$ ?

[alcoholist]

popolznev в сообщении #900016 писал(а):

Пусть функция $F$ тождественно равна нулю. Какая у неё $ F^{-1}$ ?

Вы забыли сказать, что постоянная функция на гладком многообразии бесконечно дифференцируема)))

-- Вт авг 26, 2014 00:43:24 --

loshka в сообщении #900015 писал(а):

так если отображение непрерывно дифференцируемо, то значит есть и обратное

Вы не путайте теплое с мягким обратимость с дифференцируемостью

[popolznev]

alcoholist в сообщении #900020 писал(а):

Вы забыли сказать, что постоянная функция на гладком многообразии бесконечно дифференцируема)))

поленился!

[loshka]

Цитата:

Пусть функция $F$ тождественно равна нулю. Какая у неё $ F^{-1}$ ?

Ведь якобиан этого отображения есть нуль во всех точках значит обратное отображение нельзя однозначно задать


Я ошибался думаю из того что отображение непрерывно бесконечно дифференцируемо, значит якобиан не нулевой во всех точках, наверно это не так

[popolznev]

loshka в сообщении #900053 писал(а):

Цитата:

Пусть функция $F$ тождественно равна нулю. Какая у неё $ F^{-1}$ ?

Ведь якобиан этого отображения есть нуль во всех точках значит обратное отображение нельзя однозначно задать

Я ошибался думаю из того что отображение непрерывно бесконечно дифференцируемо, значит якобиан не нулевой во всех точках, наверно это не так

Обратного отображения, конечно, у тождественной функции нет (если её область определения состоит более чем из одной точки). Но доставать по такому случаю якобиан - это совершенно лишнее, это стрельба по воробьям из пушки. Есть же просто определение обратного отображения, которое никаких якобианов не предполагает и которое очевидно применяется к тождественной функции.

Можем для определенности рассматривать функции $\mathbb{R}^2 \to \mathbb{R}$.

[alcoholist]

popolznev в сообщении #900056 писал(а):

у тождественной функции

тождественное отображение -- это $f(x)=x$, не путайте с постоянной функцией:))

[popolznev]

alcoholist в сообщении #900121 писал(а):

popolznev в сообщении #900056 писал(а):

у тождественной функции

тождественное отображение -- это $f(x)=x$, не путайте с постоянной функцией:))

это правда, нехорошо написал