ЗадачаВоспользовавшись алгоритмом смешанного генератора, сформировать последовательность

чисел, имеющих равномерное распределение на интервале

, и проверить основные статистические характеристики полученных последовательностей.
Исходные данные:


 Решение
РешениеАлгоритм смешанного генератора имеет следующий вид:

где множитель

, приращение

и модуль

, а также получаемые числа

– целые числа.
Положим

. Тогда

По целым числам последовательности
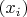
можно построить последовательность

рациональных чисел из единичного интервала.


Воспользовавшись программой Mathcad, сформируем последовательности
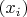
и

(Таблица 1).
Таблица 1.

Из текста задачи: "проверить основные статистические характеристики полученных последовательностей".
1. "основные" - это какие?
2. Какой вид должны иметь формулы, в которые я подставлю значения из Таблицы 1?
3. Проверка, насколько я понимаю, подразумевает сравнение. С чем мне сравнивать то, что у меня получилось?
(Оффтоп)
Ниже написал немного мыслей, которые могут быть очень неправильными.
Математическое ожидание - одна из основных статистических характеристик.
В данном случае математическое ожидание это среднее арифметическое.
![$$M[X]= \frac{\sum^{49}_{i=0}\frac {x_i}{700}}{50}=0.349$$ $$M[X]= \frac{\sum^{49}_{i=0}\frac {x_i}{700}}{50}=0.349$$](https://dxdy-03.korotkov.co.uk/f/e/c/4/ec4660959e3c66b5f06a528c68b46d5782.png)
В учебнике (см. оффтоп) на стр. 67 написано, что "среднее значение чисел не должно существенно отличаться от

"
У меня существенно отличается?
Я очень запутался
