Уважаемый
Феликс Шмидель!Рассмотрим подробно случай

.
Возмем первое уравнение с полином 4-степени относительно переменной

:

,
где

,

и

симметрические полиномы второй, третьей и четвертой степени для корней

,

,
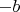
и

, и соответственно после упрощения

,

и

.
Второе уравнение с полином третьей степени относительно переменной

:

. Следует из формулы Варинга для суммы

-степеней корней первого уравнения для

:

и равенства

. Общим корнем для двух уравнений является сумма

.
Деление полинома 4 степени на полином 3, получим в остатке полином 2 степени с тем же корнем.
Можно выполнить, например, столбиком (что-то у меня столбики разъезжаются):

|

- -----------------

|

---------------------


, частное

, остаток

,

является корнем последнего квадратного уравнения.
Далее аналогично

|


-----------------

|

----------------------------

-

------------------------------------------


, и

- линейный остаток,

является также корнем остатка от деления.
Таким образом,

или

.
Дробь справа должна быть сократимой, так как слева целое число.
Пусть числитель и знаменатель имеют хотя бы один общий делитель простое число

, которое не является делителем

, и соответственно не является делителем

, то имеем

и

по модулю

.
Поделим числитель на

, а знаменатель на

, получим

и

,
где

,

,

. Деление на

, конечно, по модулю

.
Аналогично поступим с первым и вторым уравнениями, подставив в уравнения корень

, получим

и

или

и

.
Далее из 2-х последних

, а из

и

получим

или

.
Итак

, отсюда

.
Из

и

получим

. Если

, то из

получим

и

.
Получено противоречие - одновременно

и

по модулю

(очевидно, что

не равно 2 или 3, так как среди делителей

есть обязательно 2 и 3).