Вот простейшее доказательство только для части случаев.
Пусть

и

- случайные натуральные числа, удовлетворяющие условию делимости разности соответствующих кубов и квадратов:

,

и

Требуется доказать, что

Заметим, что для доказательства, можно рассматривать оба представления:
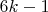
и

.
Предположим обратное:

, тогда получим, что



Перегруппировав, получим

Левая часть делится без остатка на 6, а правая, учитывая, что обратное требованию исходной задачи предположение может быть верно, делится без остатка на 6 только в том случае, если

.
Таким образом, получаем, что

, что противоречит произвольному выбору начального
