Доказать, что 3 делит разницу двух натуральных чисел.

[ghetto]

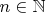
Пусть $n = a_ka_{k -1} \ldots a_1a_0$, where $n \in \mathbb N$. Докажите что если $m = a_k + a_{k -1} + \ldots + a_1 + a_0$ , тогда $n \equiv m \pmod 3$.
-

Думаю сначала показать, что $3|m$. Затем доказать $3|m \to 3|n$ из чего легко следует $3|n - m$.

Дано: $m = a_k + a_{k -1} + \ldots + a_1 + a_0$.

Делится ли $m$ на $3$? Если да, то как мы это докажем?

Известно, что $3|m \to 3j = a_k + a_{k -1} + \ldots + a_1 + a_0$ for some $j \in \mathbb Z$.

Значит ли это, что $j = \frac {a_k + a_{k -1} + \ldots + a_1 + a_0}{3}$? Если нет, то как найти $j$?

Если все что выше написано неверно, как все это доказывается?

[kp9r4d]

$1\cdot1 \neq 1+1 \pmod 3$

[ghetto]

kp9r4d в сообщении #890475 писал(а):

$1\cdot1 \neq 1+1 \pmod 3$

Это значит, что утверждение о том, что $3$ делит разницу двух натуральных чисел неверно? Может я что-то не правильно написал в описаний проблемы? Каждое $a_i$- целое base 10 число.

[Otta]

ghetto в сообщении #890473 писал(а):

Пусть $n = a_ka_{k -1} \ldots a_1a_0$, where $n \in \mathbb N$. Докажите что если $m = a_k + a_{k -1} + \ldots + a_1 + a_0$ , тогда $n \equiv m \pmod 3$.

Имелось в виду Пусть $n = \overline{a_ka_{k -1} \ldots a_1a_0}$.

[Mathusic]

(Оффтоп)

$10^k \pmod 3$

[ghetto]

$\ n = a_k 10^k + \cdots + a_1 10 + a_0 = f(10)\,$ есть полином $\,f\,$ in $10$ с коэфициентами $\,a_i.\,$ Тогда, $\,{\rm mod}\ 3\!:\ \color{#c00}{10\equiv 1}\,\Rightarrow\,f(\color{#c00}{10})\equiv f(\color{#c00}1) = a_k + \cdots + a_1 + a_0$.

Какое отношение $n =a_k 10^k + \cdots + a_1 10 + a_0$ имеет к $n_1 = a_k \ldots a_aa_0$? Может они равны? Если да, то как это показать?

[Otta]

ghetto
Вы не поняли?

Otta в сообщении #890479 писал(а):

Имелось в виду "Пусть $n = \overline{a_ka_{k -1} \ldots a_1a_0}$"

а не то, что у Вас $n_1 = a_k \ldots a_1a_0$.
Может, Вам незнакомо обозначение $n = \overline{a_ka_{k -1} \ldots a_1a_0}$? Так обозначается число в десятичной записи с цифрами $a_k,a_{k -1}, \ldots, a_1,a_0$, если читать слева направо.

[ghetto]

Otta в сообщении #890813 писал(а):

ghetto
Может, Вам незнакомо обозначение $n = \overline{a_ka_{k -1} \ldots a_1a_0}$? Так обозначается число в десятичной записи с цифрами $a_k,a_{k -1}, \ldots, a_1,a_0$, если читать слева направо.

Пожалуйста обьясните каким образом $n = \overline{a_ka_{k -1} \ldots a_1a_0}$ равняется $n =a_k 10^k + \cdots + a_1 10 + a_0$. Я так и не понял.

[Otta]

Пожалуйста. $911=9\cdot 10^2+1\cdot 10^1+1\cdot 10^0$
$n=\overline{a_2a_1a_0},\; a_2=9,\,a_1=1,\,a_0=1$.

[ghetto]

Otta в сообщении #891900 писал(а):

Пожалуйста. $911=9\cdot 10^2+1\cdot 10^1+1\cdot 10^0$
$n=\overline{a_2a_1a_0},\; a_2=9,\,a_1=1,\,a_0=1$.

Thank you.