О функции распределения простых чисел

[vvv369]

В сообщении будет рассмотрена функция распределения простых чисел, гипотеза Брокарда, доказана вторая гипотеза Харди — Литлвуда.
Сообщение было изменено, в частности, вместо $\sum\limits_{p_n}\left\lfloor\frac{x}{p}\right\rfloor$ было введено обозначение $\left\lfloor\Omega(x,p_n)\right\rfloor$ (как предложил в замечании Sonic86). Из-за большого объема текста часть первоначального сообщения будет вынесена в самостоятельное.
Обозначения:

$\pi(x)$ - количество простых чисел на интервале от 0 до $x$.
$\left\lfloor\frac{x}{p} \right\rfloor$ - целая часть от деления $\frac{x}{p}$

Краткая теория
Рассмотрим формулу Лежандра http://mathworld.wolfram.com/LegendresFormula.html

$\varphi(x,a)=\left\lfloor{x}\right\rfloor-\left\lfloor\frac{x}{p_n}\right\rfloor+\left\lfloor\frac{x}{p_np_i}\right\rfloor-\left\lfloor\frac{x}{p_np_ip_j}\right\rfloor+...,$
При $a= \pi(\sqrt{x})$
$\varphi(x,\pi(\sqrt{x}))=\pi(x)-\pi(\sqrt{x})+1=\left\lfloor{x}\right\rfloor-\sum\limits_{p_n\leqslant \sqrt{x}}\left\lfloor\frac{x}{p_n}\right\rfloor+\sum\limits_{p_i<p_n\leqslant\sqrt{x}}\left\lfloor\frac{x}{p_np_i}\right\rfloor-\sum\limits_{p_j<p_i<p_n\leqslant\sqrt{x}}\left\lfloor\frac{x}{p_np_ip_j}\right\rfloor+...$(1)

Перегруппируем правые члены сумм в данной формуле с одинаковыми $p_n$, получим, что

$$-\sum\limits_{p_n\leqslant\sqrt{x}}\left\lfloor\frac{x}{p_n}\right\rfloor +\sum\limits_{p_i<p_n\leqslant\sqrt{x}}\left\lfloor\frac{x}{p_np_i}\right\rfloor-\sum\limits_{p_j<p_i<p_n\leqslant\sqrt{x}}\left\lfloor\frac{x}{p_np_ip_j}\right\rfloor+...$$=-\sum\limits_{n=1}^{\pi(\sqrt{x})}\left\lgroup\left\lfloor\frac{x}{p_n}\right\rfloor+(-1)^1\sum\limits_{p_i<p_n}\left\lfloor\frac{x}{p_np_i} \right\rfloor+(-1)^2\sum\limits_{p_j<p_i<p_n}\left\lfloor\frac{x}{p_np_ip_j}\right\rfloor...+(-1)^{n-1}\left\lfloor\frac{x}{p_1p_2p_3...p_n}\right\rfloor\right\rgroup$$

Введем функцию
$\left\lfloor\Omega(x,p_n)\right\rfloor= -(\varphi(x,p_n) - \varphi(x,p_{n-1}) )=\left\lfloor\frac{x}{p_n}\right\rfloor+$(-1)^1\sum\limits_{p_i<p_n}\left\lfloor\frac{x}{p_np_i}\right\rfloor+(-1)^2\sum\limits_{p_j<p_i<p_n}\left\lfloor\frac{x}{p_np_ip_j}\right\rfloor+...+(-1)^{n-1}\left\lfloor\frac{x}{p_1p_2p_3...p_n}\right\rfloor$ (2)
Каждое слагаемое (2) определяет количество чисел на отрезке $[0,x]$, которые делятся на $p_n$ и не делятся при этом на простые числа меньше $p_n$.
Таким образом, (1) можно переписать в виде
$\pi(x)=x-\sum\limits_{p\leqslant\sqrt{x}}\left\lfloor\Omega(x,p)\right\rfloor+\pi(\sqrt{x})-1$ (3)

Теорема 1

Для любого натурального числа $x$ справедливо
$x-1=\sum\limits_{p\leqslantx}\left\lfloor\Omega(x,p)\right\rfloor$ (4)
Действительно, в правой части уравнения (3) стоит количество чисел на интервале от нуля до $x$, за исключением единицы.

Так как для любого $\sqrt{x}<p \leqslant x$ на интервале $[0,x]$ только само число $p$ не делится на меньшие простые числа, а все остальные числа, в разложении которых есть $p$, делятся также на другие простые числа меньше $\sqrt{x}$, то для таких простых чисел
$\left\lfloor \Omega(x,p)\right\rfloor = 1$ (5)

Если $x<p$ то $\left\lfloor \Omega(x,p)\right\rfloor = 0$

Из (3), (4) и (5) следует, что
$\sum\limits_{\sqrt{x}<p\leqslant x}\left\lfloor \Omega(x,p)\right\rfloor =\pi(x)-\pi(\sqrt{x})$ (6)
где $p$ пробегает все значения на интервале $\sqrt{x}<p\leqslant x$

Теорема 2

Количество простых чисел на отрезке $[0,2n]$

$2\pi(n)-\pi(\sqrt n) \geqslant \pi(2n) \geqslant 2\pi(n) - 2\pi(\sqrt n) - (\pi(\sqrt{2n})-\pi(\sqrt n))\cdot \left ( \pi(2\sqrt n) - \pi(\sqrt n) - \frac{\pi(\sqrt{2n})-\pi(\sqrt n)-1}{2} \right )$

Доказательство

Пусть $n$ - натуральное, запишем функцию распределения в виде
$\pi(2n) =2n - \sum\limits_{p \leqslant \sqrt {2n}}\left\lfloor \Omega(2n,p)\right\rfloor + \pi (\sqrt {2n}) -1$ и

$\pi(n) =n - \sum\limits_{p \leqslant \sqrt n}\left\lfloor \Omega(n,p)\right\rfloor + \pi (\sqrt n) -1$

Следовательно,
$\pi(2n) = 2\pi(n) - 2\pi(\sqrt n) + \pi(\sqrt {2n}) + 2\sum\limits_{p \leqslant \sqrt n} \left\lfloor \Omega(n,p)\right\rfloor - \sum\limits_{p \leqslant \sqrt {2n}} \left\lfloor \Omega(2n,p)\right\rfloor +1$
Так как
$\sum\limits_{p\leqslant \sqrt {2n}}\left\lfloor \Omega(2n,p)\right\rfloor = \sum\limits_{\sqrt n<p\leqslant \sqrt {2n}} \left\lfloor \Omega(2n,p)\right\rfloor + \sum\limits_{p\leqslant \sqrt n} \left\lfloor \Omega(2n,p)\right\rfloor$
то
$\pi(2n) = 2\pi(n) - 2\pi(\sqrt n) + \pi(\sqrt {2n}) + 2\sum\limits_{p \leqslant \sqrt n} \left\lfloor \Omega(n,p)\right\rfloor - \sum\limits_{\sqrt n<p \leqslant \sqrt {2n}} \left\lfloor \Omega(2n,p)\right\rfloor - \sum\limits_{p \leqslant \sqrt n} \left\lfloor \Omega(2n,p)\right\rfloor +1$ (7)

Рассмотрим $\sum\limits_{\sqrt n< p \leqslant \sqrt {2n}} \left\lfloor \Omega(2n,p)\right\rfloor$
Данная сумма определяет количество чисел, делящихся на простые числа $\sqrt {n} <p_m \leqslant \sqrt {2n}$ , и не делящихся на простые числа меньше $\sqrt n$ .
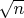
Поскольку для любого такого числа выполняется условие $p_m\cdot{p_{m+i}} \cdot{p_{m+j}}>2n$ , где $i, j \ge 0$ , то такие числа имеют вид либо $p_m$ , либо $p_m\cdot{p_{m+i}}$.
Оценим их количество. Заметим, что для любого простого числа $\sqrt{n} <p_m \leqslant \sqrt {2n}$ выполняется $2p_m\cdot{p_m} >2n$ , следовательно, на отрезке $[0,2n]$ могут лежать составные числа вида $p_m\cdot{p_{m+i}}$ , только если $p_{m+i}<2p_m$
Количество простых чисел, для которых $\sqrt{n} <p_m \leqslant \sqrt {2n}$ равно $\pi(\sqrt {2n})-\pi(\sqrt n)$, количество простых чисел $p_{m+i}$ равно $\pi(2\sqrt {n})-\pi(\sqrt {n})$, , следовательно, количество чисел

1.На отрезке $[0,n]$ вида $p_m$ равно $\pi(\sqrt {2n}) -\pi(\sqrt n)$
2. На отрезке $[n+1,2n]$ вида $p_m \cdot p_{m+i}$ меньше или равно
$(\pi(\sqrt{2n})-\pi(\sqrt n))\cdot \left ( \pi(2\sqrt n) - \pi(\sqrt n) - \frac{\pi(\sqrt{2n})-\pi(\sqrt n)-1}{2} \right )$

Тогда
$\pi(\sqrt {2n})-\pi(\sqrt n) \leqslant \sum\limits_{\sqrt n< p \leqslant \sqrt {2n}} \left\lfloor \Omega(2n,p)\right\rfloor \leqslant \pi(\sqrt {2n})-\pi(\sqrt n) - (\pi(\sqrt{2n})-\pi(\sqrt n))\cdot \left ( \pi(2\sqrt n) - \pi(\sqrt n) - \frac{\pi(\sqrt{2n})-\pi(\sqrt n)-1}{2} \right )$ (8)

Перепишем уравнение (7) в виде:
$\pi(2n) = 2\pi(n) - 2\pi(\sqrt n) + \pi(\sqrt {2n}) + \sum\limits_{p \leqslant \sqrt n} \left\lfloor \Omega(n,p)\right\rfloor - \left ( \sum\limits_{p \leqslant \sqrt n} \left\lfloor \Omega(2n,p)\right\rfloor - \sum\limits_{p \leqslant \sqrt n} \left\lfloor \Omega(n,p)\right\rfloor \right ) - \sum\limits_{\sqrt n<p \leqslant \sqrt {2n}} \left\lfloor \Omega(2n,p)\right\rfloor +1$(9)

Сравним $\sum\limits_{p \leqslant \sqrt n} \left\lfloor \Omega(2n,p)\right\rfloor - \sum\limits_{p \leqslant \sqrt n} \left\lfloor \Omega(n,p)\right\rfloor и \sum\limits_{p \leqslant \sqrt n} \left\lfloor \Omega(n,p)\right\rfloor$

Первая из величин равна количеству чисел на отрезке $[n+1,2n]$ , причем таких, которые делятся на простые числа $p\leqslant \sqrt n$.
Сумма $\sum\limits_{p \leqslant \sqrt n} \left\lfloor\Omega(n,p)\right\rfloor$ показывает количество таких же чисел на отрезке $[0,n]$.
Поскольку длина отрезка $[0,n]$ такая же, как и длина отрезка $[n+1,2n]$, то количество чисел на втором отрезке, делящихся на $p \leqslant \sqrt n$, равно или больше на единицу, чем количество таких же чисел на первом отрезке. Кроме того, на отрезке $[n+1,2n]$ число $n+1$ может делиться на $p\leqslant \sqrt n$, а единица на отрезке $[0,n]$ на это $p$ не делится. Следовательно,

$\sum\limits_{p \leqslant \sqrt n}\left\lfloor \Omega(n,p)\right\rfloor \leqslant \sum\limits_{p \le \sqrt n} \left\lfloor \Omega(2n,p)\right\rfloor- \sum\limits_{p \leqslant \sqrt n} \left\lfloor\Omega(n,p)\right\rfloor -1 \leqslant \sum\limits_{p \leqslant \sqrt n} \left\lfloor\Omega(n,p)\right\rfloor +\pi(\sqrt n)$

Из этого условия, условия (8) и из уравнения (9) получим, что

$2\pi(n)-\pi(\sqrt n) \geqslant \pi(2n) \geqslant 2\pi(n) - 2\pi(\sqrt n) - (\pi(\sqrt{2n})-\pi(\sqrt n))\cdot \left ( \pi(2\sqrt n) - \pi(\sqrt n) - \frac{\pi(\sqrt{2n})-\pi(\sqrt n)-1}{2} \right )$


Гипотеза Брокарда.
Для любого натурального $n$ между $p_n^2$ и $p_{n+1}^2$ (где $p_n$ — это $n$-ое простое число) найдётся хотя бы четыре простых числа

Теорема 3

Для любого натурального $n$ между $p_n^2$ и $p_{n+1}^2$ (где $p_n$ — это $n$-ое простое число)

$\pi(p_{n+1}^2-p_n^2) -2n -2 \leqslant \pi(p_{n+1}^2)-\pi(p_n^2) \leqslant \pi(p_{n+1}^2-p_n^2) -n -1$

Доказательство

Из функции распределения простых чисел (3) следует, что
$\pi(p_n^2) =p_n^2 - \sum\limits_{p \leqslant p_n} \left\lfloor \Omega(p_n^2,p)\right\rfloor + n -1$
$\pi(p_{n+1}^2) =p_{n+1}^2 - \sum\limits_{p \leqslant p_{n+1}} \left\lfloor \Omega(p_{n+1}^2,p)\right\rfloor + n$

Их разность
$\pi(p_{n+1}^2) - \pi(p_n^2) =p_{n+1}^2 - p_n^2 -\sum\limits_{p \leqslant p_{n+1}} \left\lfloor \Omega(p_{n+1}^2,p)\right\rfloor +\sum\limits_{p \leqslant p_n} \left\lfloor\Omega(p_n^2,p)\right\rfloor +1$(10)

Так как $\left\lfloor \Omega(p_n^2,p_{n+1})\right\rfloor =1$
то
$\sum\limits_{p \leqslant p_n} \left\lfloor\Omega(p_n^2,p)\right\rfloor +1 =\sum\limits_{p \leqslant p_{n+1}} \left\lfloor \Omega(p_n^2,p)\right\rfloor$

С учетом этого перепишем (10)
$\pi(p_{n+1}^2) - \pi(p_n^2) =p_{n+1}^2 - p_n^2 -\sum\limits_{p \leqslant p_{n+1}} \left\lfloor\Omega(p_{n+1}^2,p)\right\rfloor + \sum\limits_{p \leqslant p_{n+1}} \left\lfloor\Omega(p_n^2,p)\right\rfloor$(11)

Разность
$\sum\limits_{p \leqslant p_{n+1}} \left\lfloor \Omega(p_{n+1}^2,p)\right\rfloor - \sum\limits_{p \leqslant p_{n+1}} \left\lfloor\Omega(p_n^2,p)\right\rfloor$
равна количеству чисел на отрезке $[p_n^2+1 ,p_{n+1}^2]$ , причем таких, которые делятся на простые числа $p\leqslant p_{n+1}$.
Величина $\sum\limits_{p \leqslant p_{n+1}} \left\lfloor \Omega(p_{n+1}^2-p_n^2,p)\right\rfloor$ показывает количество таких же чисел на отрезке $[0, p_{n+1}^2-p_n^2]$.
Поскольку длина обоих отрезков одинакова, то количество чисел на отрезке $[p_n^2+1 ,p_{n+1}^2]$, делящихся на простое число $p\leqslant p_{n+1}$, равно или больше на единицу, чем количество таких чисел на другом отрезке. Учтем, что на отрезке $[p_n^2+1,p_{n+1}^2]$ число $p_n^2+1$ может делиться на $p\leqslant p_{n+1}$, а единица на отрезке $[0, p_{n+1}^2-p_n^2]$ на такое $p$ не делится.
Количество простых чисел $p\leqslant p_{n+1}$ равно $n+1$. Следовательно,

$$\sum\limits_{p \leqslant p_{n+1}} \left\lfloor \Omega(p_{n+1}^2-p_n^2,p)\right\rfloor\leqslant \sum\limits_{p \leqslant p_{n+1}} \left\lfloor\Omega(p_{n+1}^2,p)\right\rfloor - \sum\limits_{p \leqslant p_{n+1}} \left\lfloor \Omega(p_n^2,p)\right\rfloor -1 \leqslant \sum\limits_{p \leqslant p_{n+1}} \left\lfloor \Omega(p_{n+1}^2-p_n^2,p)\right\rfloor+n + 1$$

(11)


Тогда из (10) с учетом (11) получим

$$p_{n+1}^2 - p_n^2 - \sum\limits_{p \leqslant p_{n+1}} \left\lfloor \Omega(p_{n+1}^2-p_n^2,p)\right\rfloor -n - 2\leqslant \pi(p_{n+1}^2) - \pi(p_n^2) \leqslant p_{n+1}^2 - p_n^2 - \sum\limits_{p \leqslant p_{n+1}} \left\lfloor \Omega(p_{n+1}^2-p_n^2,p)\right\rfloor -1$$

(12)
Согласно теореме 1
$p_{n+1}^2 - p_n^2-1 = \sum\limits_{p \leqslant p_{n+1}^2-p_n^2} \left\lfloor\Omega(p_{n+1}^2-p_n^2,p)\right\rfloor = \sum\limits_{n+2<p \leqslant p_{n+1}^2-p_n^2} \left\lfloor\Omega(p_{n+1}^2-p_n^2,p)\right\rfloor + \sum\limits_{p \leqslant n+1} \left\lfloor\Omega(p_{n+1}^2-p_n^2,p)\right\rfloor$

Но так как $$\pi(p_{n+1}^2-p_n^2) > n +1$ и для любого $p>p_{n+1}$
$\left\lfloor\Omega(p_{n+1}^2-p_n^2,p)\right\rfloor=1$$, то

\sum\limits_{n+2<p \leqslant p_{n+1}^2-p_n^2} \left\lfloor\Omega(p_{n+1}^2-p_n^2,p)\right\rfloor = \pi(p_{n+1}^2-p_n^2) - n -1$
Следовательно,

$\pi(p_{n+1}^2-p_n^2) =p_{n+1}^2 - p_n^2-\sum\limits_{p \leqslant p_{n+1}} \left\lfloor\Omega(p_{n+1}^2-p_n^2,p)\right\rfloor + n$

и неравенство (12) преобразуется в
$\pi(p_{n+1}^2-p_n^2) -2n -2 \leqslant \pi(p_{n+1}^2)-\pi(p_n^2) \leqslant \pi(p_{n+1}^2-p_n^2) -n -1$

Вторая гипотеза Харди — Литлвуда

Докажем, что
$\pi(x+y)-\pi(x) \leqslant \pi(y)$

Доказательство

Случай $x =y$ рассмотрен в теореме 2.
Пусть $x >y$.
Поскольку
$(x+y)-x = y$
То согласно теореме 1
$\sum\limits_{p\leqslant x+y} \left\lfloor \Omega(x+y,p) \right\rfloor - \sum\limits_{p\leqslant x} \left\lfloor \Omega(x,p) \right\rfloor = \sum\limits_{p\leqslant y} \left\lfloor \Omega(y,p) \right\rfloor + 1$ (13)

Тогда

$$\sum\limits_{\sqrt{x+y}<p\leqslant x+y} \left\lfloor \Omega(x+y,p) \right\rfloor + \sum\limits_{p\leqslant \sqrt{x+y}} \left\lfloor \Omega(x+y,p)\right\rfloor - \sum\limits_{\sqrt{x}<p\leqslant x} \left\lfloor \Omega(x,p)\right\rfloor -\sum\limits_{p\leqslant \sqrt{x}} \left\lfloor \Omega(x,p)\right\rfloor $= \sum\limits_{\sqrt{y}<p\leqslant y} \left\lfloor \Omega(y,p)\right\rfloor +\sum\limits_{p\leqslant \sqrt{y}} \left\lfloor \Omega(y,p)\right\rfloor + 1$$

Или

$$\pi(x+y) -\pi(\sqrt{x+y}) + \sum\limits_{p\leqslant \sqrt{x+y}} \left\lfloor \Omega(x+y,p) \right\rfloor - \pi(x) +\pi(\sqrt{x}) - \sum\limits_{p\leqslant \sqrt{x}} \left\lfloor\Omega(x,p)\right\rfloor =$ \pi(y) -\pi(\sqrt{y}) + \sum\limits_{p\leqslant \sqrt{y}} \left\lfloor\Omega(y,p)\right\rfloor + 1$$

$$\pi(x+y) - \pi(x) +\pi(\sqrt{x}) +\pi(\sqrt{y}) -\pi(\sqrt{x+y}) + \sum\limits_{\sqrt{x} <p\leqslant \sqrt{x+y}} \left\lfloor \Omega(x+y,p)\right\rfloor + \sum\limits_{p\leqslant \sqrt{x}} \left\lfloor\Omega(x+y,p)\right\rfloor-$ \sum\limits_{p\leqslant \sqrt{x}} \left\lfloor \Omega(x,p)\right\rfloor - \sum\limits_{p\leqslant \sqrt{y}} \left\lfloor \Omega(y,p) \right\rfloor - 1= \pi(y)$$

(14)

Сумма $\sum\limits_{\sqrt{x} <p\leqslant \sqrt{x+y}} \left\lfloor\Omega(x+y,p)\right\rfloor \geqslant 0$ (15)

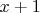
Величина $\sum\limits_{p\leqslant \sqrt{x}} \left\lfloor \Omega(x+y,p)\right\rfloor- \sum\limits_{p\leqslant \sqrt{x}} \left\lfloor\Omega(x,p)\right\rfloor$ равна количеству чисел на интервале $[x,x+y]$ , причем таких, которые делятся на простые числа $p \leqslant \sqrt{x+y}$. Кроме того, на интервале $[x,x+y]$ число $x+1$ может делиться на $p\leqslant \sqrt{x}$, а единица на интервале $[0,y]$ на такое $p$ не делится.

Величина $\sum\limits_{p\leqslant \sqrt{y}} \left\lfloor\Omega(y,p)\right\rfloor$ показывает количество чисел, которые делятся на простые числа $p\leqslant \sqrt{y}$ на интервале $[0,y]$ .

Поскольку длины первого и второго интервалов одинаковы, а по условию $x\geqslant y$ , то
$\sum\limits_{p\leqslant \sqrt{x}} \left\lfloor \Omega(x+y,p)\right\rfloor- \sum\limits_{p\leqslant \sqrt{x}} \left\lfloor \Omega(x,p)\right\rfloor \geqslant \sum\limits_{p\leqslant \sqrt{y}} \left\lfloor\Omega(y,p)\right\rfloor +1$ (16)
Так как
$\sqrt{x}+\sqrt{y} \geqslant \sqrt{x+y}$ то
$\pi(\sqrt{x}) +\pi(\sqrt{y})- \pi(\sqrt{x+y}) \geqslant 0$ (17)

Из (14) с учетом (15), (16), (17) окончательно получим
$\pi(x+y) - \pi(x) \leqslant \pi(y)$

Рассуждая таким же образом для случая $x \geqslant y$ и $\sqrt{x+y} < y$ получим, что

$\pi(x+y) - \pi(x) +\pi(\sqrt{y}) \leqslant \pi(y)$

Случай $x \leqslant y$ также доказывается аналогично

[Sonic86]

vvv369 в сообщении #862683 писал(а):

Вторая гипотеза Харди — Литлвуда

Докажем, что
$\pi(x+y)-\pi(x) \leqslant \pi(y)$
Доказательство

Она ложная скорее всего: http://en.wikipedia.org/wiki/Second_Har ... conjecture

А вообще текст неструктурированный, могли бы и получше написать.
И доллары надо ставить.

vvv369 в сообщении #862683 писал(а):

$\sum\limits_{p_{n+1}} \left\lfloor \frac{p_n^2}{p}\right\rfloor =1$

Какая область суммирования в сумме слева?

vvv369 в сообщении #862683 писал(а):

Так как $\sum\limits_{p_{n+1}} \left\lfloor \frac{p_n^2}{p}\right\rfloor =1$
то
$\sum\limits_{p \leqslant p_n} \left\lfloor \frac{p_n^2}{p}\right\rfloor +1 =\sum\limits_{p \leqslant p_{n+1}} \left\lfloor \frac{p_n^2}{p}\right\rfloor$

Ага, похоже, что автор считает, что $\sum\limits_{p=p_{n+1}} \left\lfloor \frac{p_n^2}{p}\right\rfloor =1$.
Это неверно.
Дальше не читал.

[vvv369]

Цитата:

Она ложная скорее всего: http://en.wikipedia.org/wiki/Second_Har ... conjecture

Ну у меня получилось так. Если конечно мои рассуждения верны.

[vvv369]

Sonic86 в сообщении #862698 писал(а):

Цитата:

vvv369 в сообщении #862683
писал(а):
$\sum\limits_{p_{n+1}} \left\lfloor \frac{p_n^2}{p}\right\rfloor =1$

Какая область суммирования в сумме слева?

vvv369 в сообщении #862683
писал(а):

Цитата:

Так как $\sum\limits_{p_{n+1}} \left\lfloor \frac{p_n^2}{p}\right\rfloor =1$
то
$\sum\limits_{p \leqslant p_n} \left\lfloor \frac{p_n^2}{p}\right\rfloor +1 =\sum\limits_{p \leqslant p_{n+1}} \left\lfloor \frac{p_n^2}{p}\right\rfloor$

Ага, похоже, что автор считает, что $\sum\limits_{p=p_{n+1}} \left\lfloor \frac{p_n^2}{p}\right\rfloor =1$.
Это неверно.

Суммирование я обозначил так:
если под знаком суммы стоит определенное число, например $p_n$, то суммирование ведется по формуле (2)
$\sum\limits_{p_n}\left\lfloor\frac{x}{p}\right\rfloor = \left\lfloor \frac{x} {p_n} \right\rfloor + $(-1)^1 \sum\limits_{i=1}^{n-1} \left\lfloor \frac{x}{p_np_i} \right\rfloor+ (-1)^2 \sum\limits_{i,j=1,i\neq{j}}^{n-1} \left\lfloor \frac{x}{p_np_ip_j} \right\rfloor +(-1)^3 \sum\limits_{i,j,k=1,i\neq{j}\neq{k}}^{n-1} \left\lfloor \frac{x}{p_np_ip_jp_k} \right\rfloor+...+ (-1)^{n-1}\left\lfloor\frac{x}{p_1p_2p_3...p_n}\right\rfloor$
Это количество чисел на интервале $[0,x]$, которые делятся на $p_n$ но не делятся при этом на простые числа меньше $p_n$ (они вычитаются)

Данная формула получается, если в члене $ \sum\limits_{p_n \leqslant \sqrt{x}}\left\lfloor \frac{x}{p} \right\rfloor $ формулы Лежандра выделить все слагаемые с $p_n$


Если под знаком суммы стоит неравенство, например $ p_i<p_n \leqslant p_j $, то суммирование ведется по формуле
$ \sum\limits_{p_i<p_n \leqslant p_j}\left\lfloor \frac{x}{p} \right\rfloor = \sum\limits_{n=i+1}^ {j} \sum\limits_{p_n} \left\lfloor \frac{x}{p}\right\rfloor$
Это количество чисел на интервале $[0,x]$, которые делятся на простые числа $ p_i<p_n \leqslant p_j $, но не делятся на меньшие простые числа

Поэтому
$\sum\limits_{p= p_{n+1} } \left\lfloor \frac{p_n^2}{p}\right\rfloor = \left\lfloor \frac{p_n^2} {p_{n+1}} \right\rfloor + $(-1)^1 \sum\limits_{i=1}^{n} \left\lfloor \frac{p_n^2}{p_{n+1} p_i} \right\rfloor+ (-1)^2 \sum\limits_{i,j=1,i\neq{j}}^{n} \left\lfloor \frac{p_n^2}{p_{n+1} p_ip_j} \right\rfloor +(-1)^3 \sum\limits_{i,j,k=1,i\neq{j}\neq{k}}^{n} \left\lfloor \frac{p_n^2}{p_{n+1} p_ip_jp_k} \right\rfloor+...+ (-1)^{n}\left\lfloor\frac{p_n^2}{p_1p_2p_3...p_{n+1}}\right\rfloor $


На интервале $[0,p_n^2]$ имеется только одно число, в разложении которого есть $p_{n+1}$ и которое не делится на меньшие простые числа: это само $p_{n+1}$, все остальные числа, в разложении которых есть $p_{n+1}$, делятся также на другие простые числа.
Следовательно

$\sum\limits_{p=p_{n+1}} \left\lfloor \frac{p_n^2}{p}\right\rfloor =1$.
Например, если $p_{n+1} = 7$ получим

$\sum\limits_{p_{n+1}= 7 } \left\lfloor \frac{25}{p}\right\rfloor = \left\lfloor \frac{25} {7} \right\rfloor - \left\lfloor \frac{25}{2 \cdot 7 } \right\rfloor - \left\lfloor \frac{25}{3 \cdot 7 } \right\rfloor - \left\lfloor \frac{25}{5 \cdot 7 } \right\rfloor + \left\lfloor \frac{25}{2 \cdot 3 \cdot 7 } \right\rfloor + \left\lfloor \frac{25}{2 \cdot 5 \cdot 7 } \right\rfloor +\left\lfloor \frac{25}{3 \cdot 5 \cdot 7 } \right\rfloor - \left\lfloor \frac{25}{2 \cdot 3 \cdot 5 \cdot 7 } \right\rfloor = 3-1-1 = 1$

Прошу простить плохую структурированность моего текста, а также запутанность обозначений, ввел их для простоты записи.

[Sonic86]

Так Вы введите какое-нибудь явное обозначение, типа

$$\Omega(x,p_n):= \left\lfloor \frac{x} {p_n} \right\rfloor + (-1)^1 \sum\limits_{i=1}^{n-1} \left\lfloor \frac{x}{p_np_i} \right\rfloor+ (-1)^2 \sum\limits_{i,j=1,i\neq{j}}^{n-1} \left\lfloor \frac{x}{p_np_ip_j} \right\rfloor +...+ (-1)^{n-1}\left\lfloor\frac{x}{p_1p_2p_3...p_n}\right\rfloor$$

и пользуйтесь. И текст понятный будет.

[vvv369]

Sonic86 в сообщении #863187 писал(а):

Так Вы введите какое-нибудь явное обозначение, типа

$$\Omega(x,p_n):= \left\lfloor \frac{x} {p_n} \right\rfloor + (-1)^1 \sum\limits_{i=1}^{n-1} \left\lfloor \frac{x}{p_np_i} \right\rfloor+ (-1)^2 \sum\limits_{i,j=1,i\neq{j}}^{n-1} \left\lfloor \frac{x}{p_np_ip_j} \right\rfloor +...+ (-1)^{n-1}\left\lfloor\frac{x}{p_1p_2p_3...p_n}\right\rfloor$$

и пользуйтесь. И текст понятный будет.

Спасибо за замечание, обязательно учту, но я так полагаю, что переделать данный пост уже не получится.

[Deggial]

Тема перемещена из форума «Дискуссионные темы (М)» в форум «Карантин»
Причина переноса: по просьбе ТС

Тема перемещена из форума «Карантин» в форум «Дискуссионные темы (М)»
Возвращено

[vvv369]

Цитата:

В тексте неправильно отображается теорема 1
Для любого натурального числа $x$ справедливо
$x-1=\sum\limits_{p\leqslantx}\left\lfloor\Omega(x,p)\right\rfloor$ (4)

правильный вариант:
Для любого натурального числа $x$ справедливо
$x-1=\sum\limits_{p\leqslant{x}}\left\lfloor\Omega(x,p)\right\rfloor$ (4)

[Sonic86]

Пока толком не смотрел.
Интересно, зачем $\Omega$ заключена в целую часть?

[vvv369]

Sonic86 в сообщении #863887 писал(а):

Интересно, зачем $\Omega$ заключена в целую часть?

В следующей теме собираюсь ввести функции $\left\{\Omega(x,p_n)\right\} $ и $\Omega(x,p_n) $ , которые будут строиться по такому же закону, но от дробной части и от самого числа соответственно. Правильнее, конечно было бы написать так:$ \Omega(\left\lfloor x\right\rfloor,p_n)$,но наглядность, особенно в больших формулах, по-моему хуже.

$\pi(2n) = 2\pi(n) - 2\pi(\sqrt n) + \pi(\sqrt {2n}) + 2\sum\limits_{p \leqslant \sqrt n} \Omega(\left\lfloor n\right\rfloor ,p)- \sum\limits_{\sqrt n<p \leqslant \sqrt {2n}} \Omega(\left\lfloor 2n \right\rfloor ,p)- \sum\limits_{p \leqslant \sqrt n} \Omega(\left\lfloor 2n\right\rfloor ,p)+1$

[Sonic86]

vvv369 в сообщении #863945 писал(а):

В следующей теме собираюсь ввести функции $\left\{\Omega(x,p_n)\right\} $ и $\Omega(x,p_n) $ , которые будут строиться по такому же закону, но от дробной части и от самого числа соответственно.

Не очень вдумывался, но в формулировке явный баг, ибо $\forall x \forall y [\Omega(x,y)]=\Omega(x,y), \{\Omega(x,y)\}=0$

vvv369 в сообщении #862683 писал(а):

$\varphi(x,a)=\left\lfloor{x}\right\rfloor-\left\lfloor\frac{x}{p_n}\right\rfloor+\left\lfloor\frac{x}{p_np_i}\right\rfloor-\left\lfloor\frac{x}{p_np_ip_j}\right\rfloor+...,$
При $a= \pi(\sqrt{x})$
$\varphi(x,\pi(\sqrt{x}))=\pi(x)-\pi(\sqrt{x})+1=\left\lfloor{x}\right\rfloor-\sum\limits_{p_n\leqslant \sqrt{x}}\left\lfloor\frac{x}{p_n}\right\rfloor+\sum\limits_{p_i<p_n\leqslant\sqrt{x}}\left\lfloor\frac{x}{p_np_i}\right\rfloor-\sum\limits_{p_j<p_i<p_n\leqslant\sqrt{x}}\left\lfloor\frac{x}{p_np_ip_j}\right\rfloor+...$(1)

Вы в 1-й формуле для $\varphi(x,a)$ знаки сумм потеряли.

vvv369 в сообщении #862683 писал(а):

Перегруппируем правые члены сумм в данной формуле с одинаковыми $p_n$, получим, что

$$-\sum\limits_{p_n\leqslant\sqrt{x}}\left\lfloor\frac{x}{p_n}\right\rfloor +\sum\limits_{p_i<p_n\leqslant\sqrt{x}}\left\lfloor\frac{x}{p_np_i}\right\rfloor-\sum\limits_{p_j<p_i<p_n\leqslant\sqrt{x}}\left\lfloor\frac{x}{p_np_ip_j}\right\rfloor+...$$

$$=-\sum\limits_{n=1}^{\pi(\sqrt{x})}\left\lgroup\left\lfloor\frac{x}{p_n}\right\rfloor+(-1)^1\sum\limits_{p_i<p_n}\left\lfloor\frac{x}{p_np_i} \right\rfloor+(-1)^2\sum\limits_{p_j<p_i<p_n}\left\lfloor\frac{x}{p_np_ip_j}\right\rfloor...+(-1)^{n-1}\left\lfloor\frac{x}{p_1p_2p_3...p_n}\right\rfloor\right\rgroup$$

Нет, непонятно. Откуда вылезло суммирование по $n$, куда делись $[x],\pi(x),\pi(\sqrt{x})$? Тем более, что левая часть здесь - та же, что и в предыдущей формуле справа.

Самое интересное, что это все для следующего вывода не нужно:

vvv369 в сообщении #862683 писал(а):

Введем функцию

$$\left\lfloor\Omega(x,p_n)\right\rfloor= -(\varphi(x,p_n) - \varphi(x,p_{n-1}) )=\left\lfloor\frac{x}{p_n}\right\rfloor+(-1)^1\sum\limits_{p_i<p_n}\left\lfloor\frac{x}{p_np_i}\right\rfloor+(-1)^2\sum\limits_{p_j<p_i<p_n}\left\lfloor\frac{x}{p_np_ip_j}\right\rfloor+...$$

(2)
Каждое слагаемое (2) определяет количество чисел на отрезке $[0,x]$, которые делятся на $p_n$ и не делятся при этом на простые числа меньше $p_n$.
Таким образом, (1) можно переписать в виде
$\pi(x)=x-\sum\limits_{p\leqslant\sqrt{x}}\left\lfloor\Omega(x,p)\right\rfloor+\pi(\sqrt{x})-1$ (3)

Правильно писать $\Omega(x,p_n)= -(\varphi(x,n) - \varphi(x,n-1))$
Можно не писать все страшные комбинаторные суммы, а сказать, что формула следует из смысла.
Или еще проще:
Если $\Omega(x,p_k)= \varphi(x,k-1)-\varphi(x,k)$, то
$\sum\limits_{p\leqslant\sqrt{x}}\Omega(x,p)=\varphi(x,0)-\varphi(x,\pi(\sqrt{x}))=x-\pi(x)+\pi(\sqrt{x})-1$
Я обошелся без комбинаторных сумм.
Попробуйте подойти к своему тексту как программист: оптимизируйте его, найдите все ненужные формулы, тавтологии и преобразования и выбросьте - они лишь утяжеляет код. Вам самому станет понятнее, будет меньше ошибок. и люди к Вам потянутся

vvv369 в сообщении #862683 писал(а):

Для любого натурального числа $x$ справедливо
$x-1=\sum\limits_{p\leqslantx}\left\lfloor\Omega(x,p)\right\rfloor$ (4)

vvv369 в сообщении #862683 писал(а):

Из (3), (4) и (5) следует, что
$\sum\limits_{\sqrt{x}<p\leqslant x}\left\lfloor \Omega(x,p)\right\rfloor =\pi(x)-\pi(\sqrt{x})$ (6)

нормально вроде.

Дальше пока ниасилил. Многабуков.

[vvv369]

Sonic86 в сообщении #864034 писал(а):

Цитата:

vvv369 в сообщении #863945
писал(а):
В следующей теме собираюсь ввести функции $\left\{\Omega(x,p_n)\right\} $ и $\Omega(x,p_n) $ , которые будут строиться по такому же закону, но от дробной части и от самого числа соответственно.

Не очень вдумывался, но в формулировке явный баг, ибо $\forall x \forall y [\Omega(x,y)]=\Omega(x,y), \{\Omega(x,y)\}=0$

Да, некорректно сформулировал: будут строиться по такому же алгоритму. То есть
$\left\lfloor\Omega(x,p_n)\right\rfloor=\left\lfloor\frac{x}{p_n}\right\rfloor+(-1)^1\sum\limits_{p_i<p_n}\left\lfloor\frac{x}{p_np_i}\right\rfloor+(-1)^2\sum\limits_{p_j<p_i<p_n}\left\lfloor\frac{x}{p_np_ip_j}\right\rfloor+...+(-1)^{n-1}\left\lfloor\frac{x}{p_1p_2p_3...p_n}\right\rfloor$

$\left\{\Omega(x,p_n)\right\} =\left\{\frac{x}{p_n}\right\}+(-1)^1\sum\limits_{p_i<p_n}\left\{\frac{x}{p_np_i}\right\}+(-1)^2\sum\limits_{p_j<p_i<p_n}\left\{\frac{x}{p_np_ip_j}\right\}+...+(-1)^{n-1}\left\{\frac{x}{p_1p_2p_3...p_n}\right\}$

$\Omega(x,p_n)=\frac{x}{p_n}+(-1)^1\sum\limits_{p_i<p_n}\frac{x}{p_np_i}+(-1)^2\sum\limits_{p_j<p_i<p_n}\frac{x}{p_np_ip_j}+...+(-1)^{n-1}\frac{x}{p_1p_2p_3...p_n}$

тогда
$\pi(x)=x-\sum\limits_{p\leqslant\sqrt{x}}\left\lfloor\Omega(x,p)\right\rfloor+\pi(\sqrt{x})-1$
преобразовывается в
$\pi(x)= x \prod\limits_{p\leqslant \sqrt{x}} \left( 1-\frac{1}{p}\right) + \sum\limits_{p\leqslant \sqrt{x}}\left\{\Omega(x,p)\right\}+ \pi(\sqrt{x})-1$

Sonic86 в сообщении #864034 писал(а):

Можно не писать все страшные комбинаторные суммы, а сказать, что формула следует из смысла.

Для понимания, как получаются $\left\{\Omega(x,p_n)\right\}$ и $\Omega(x,p_n)$ я поэтому комбинаторные суммы оставил, а также обозначил их именно так, а не $\Omega(\left\{x\right\},p_n)$ - по моему, не так наглядно:$\Omega(\left\lfloor{x}\right\rfloor ,p_n)= \Omega(x,p_n)- \Omega(\left\{x\right\},p_n)$ . Более подробно напишу в следующей теме.

Sonic86 в сообщении #864034 писал(а):

Цитата:

vvv369 в сообщении #862683
писал(а):
Перегруппируем правые члены сумм в данной формуле с одинаковыми $p_n$, получим, что

$$-\sum\limits_{p_n\leqslant\sqrt{x}}\left\lfloor\frac{x}{p_n}\right\rfloor +\sum\limits_{p_i<p_n\leqslant\sqrt{x}}\left\lfloor\frac{x}{p_np_i}\right\rfloor-\sum\limits_{p_j<p_i<p_n\leqslant\sqrt{x}}\left\lfloor\frac{x}{p_np_ip_j}\right\rfloor+...$$

$$=-\sum\limits_{n=1}^{\pi(\sqrt{x})}\left\lgroup\left\lfloor\frac{x}{p_n}\right\rfloor+(-1)^1\sum\limits_{p_i<p_n}\left\lfloor\frac{x}{p_np_i} \right\rfloor+(-1)^2\sum\limits_{p_j<p_i<p_n}\left\lfloor\frac{x}{p_np_ip_j}\right\rfloor...+(-1)^{n-1}\left\lfloor\frac{x}{p_1p_2p_3...p_n}\right\rfloor\right\rgroup$$

Нет, непонятно. Откуда вылезло суммирование по $n$, куда делись $[x],\pi(x),\pi(\sqrt{x})$? Тем более, что левая часть здесь - та же, что и в предыдущей формуле справа.

Если расписать подробно, получается так:
$$\varphi(x,\pi(\sqrt{x}))=\pi(x)-\pi(\sqrt{x})+1=$ $\left\lfloor{x}\right\rfloor-\sum\limits_{p_n\leqslant \sqrt{x}}\left\lfloor\frac{x}{p_n}\right\rfloor+\sum\limits_{p_i<p_n\leqslant\sqrt{x}}\left\lfloor\frac{x}{p_np_i}\right\rfloor-\sum\limits_{p_j<p_i<p_n\leqslant\sqrt{x}}\left\lfloor\frac{x}{p_np_ip_j}\right\rfloor+... $ $= \left\lfloor{x}\right\rfloor -\left\lfloor\frac{x}{p_1}\right\rfloor - \left(\left\lfloor\frac{x}{p_2}\right\rfloor - \left\lfloor\frac{x}{p_1p_2}\right\rfloor \right)- \left(\left\lfloor\frac{x}{p_3}\right\rfloor - \left\lfloor\frac{x}{p_1p_3}\right\rfloor - \left\lfloor\frac{x}{p_2p_3}\right\rfloor + \left\lfloor\frac{x}{p_1p_2p_3}\right\rfloor \right)-$ $ \left(\left\lfloor\frac{x}{p_4}\right\rfloor - \left\lfloor\frac{x}{p_1p_4}\right\rfloor - \left\lfloor\frac{x}{p_2p_4}\right\rfloor - \left\lfloor\frac{x}{p_3p_4}\right\rfloor + \left\lfloor\frac{x}{p_1p_2p_4}\right\rfloor +\left\lfloor\frac{x}{p_1p_3p_4}\right\rfloor +\left\lfloor\frac{x}{p_2p_3p_4}\right\rfloor - \left\lfloor\frac{x}{p_1p_2p_3p_4}\right\rfloor \right)+... $ $= x - \sum\limits_{n=1}^{\pi(\sqrt{x})}\left(\left\lfloor\frac{x}{p_n}\right\rfloor+ (-1)^1\sum\limits_{p_i<p_n}\left\lfloor\frac{x}{p_np_i} \right\rfloor+(-1)^2\sum\limits_{p_j<p_i<p_n}\left\lfloor\frac{x}{p_np_ip_j}\right\rfloor...+(-1)^{n-1}\left\lfloor\frac{x}{p_1p_2p_3...p_n}\right\rfloor\right)$$

Sonic86 в сообщении #864034 писал(а):

Тем более, что левая часть здесь - та же, что и в предыдущей формуле справа.

Пытался сократить текст, преобразовав правую часть отдельно от всего уравнения

Sonic86 в сообщении #864034 писал(а):

Попробуйте подойти к своему тексту как программист: оптимизируйте его, найдите все ненужные формулы, тавтологии и преобразования и выбросьте - они лишь утяжеляет код. Вам самому станет понятнее, будет меньше ошибок. и люди к Вам потянутся

Спасибо за замечания. Я на форуме новичок, не подскажите, корректно ли будет исправленный текст опубликовать в комментарии, или все же исправления надо вносить через карантин?

[Deggial]

vvv369 в сообщении #864184 писал(а):

Я на форуме новичок, не подскажите, корректно ли будет исправленный текст опубликовать в комментарии, или все же исправления надо вносить через карантин?

Как угодно. Можете новый пост писать, можете попросить отправить тему в Карантин.
На форуме также есть раздел "Тестирование" - можно там писать и редактировать посты. Правила раздела описаны в нём. Там же Вам могут и ответить по формулировкам.

[Sonic86]

vvv369 в сообщении #864184 писал(а):

То есть
$\left\lfloor\Omega(x,p_n)\right\rfloor=\left\lfloor\frac{x}{p_n}\right\rfloor+(-1)^1\sum\limits_{p_i<p_n}\left\lfloor\frac{x}{p_np_i}\right\rfloor+(-1)^2\sum\limits_{p_j<p_i<p_n}\left\lfloor\frac{x}{p_np_ip_j}\right\rfloor+...+(-1)^{n-1}\left\lfloor\frac{x}{p_1p_2p_3...p_n}\right\rfloor$

$\left\{\Omega(x,p_n)\right\} =\left\{\frac{x}{p_n}\right\}+(-1)^1\sum\limits_{p_i<p_n}\left\{\frac{x}{p_np_i}\right\}+(-1)^2\sum\limits_{p_j<p_i<p_n}\left\{\frac{x}{p_np_ip_j}\right\}+...+(-1)^{n-1}\left\{\frac{x}{p_1p_2p_3...p_n}\right\}$

$\Omega(x,p_n)=\frac{x}{p_n}+(-1)^1\sum\limits_{p_i<p_n}\frac{x}{p_np_i}+(-1)^2\sum\limits_{p_j<p_i<p_n}\frac{x}{p_np_ip_j}+...+(-1)^{n-1}\frac{x}{p_1p_2p_3...p_n}$

Вы вводите обозначения некорректно.
$[\Omega(x,y)]$ - это целая часть от $\Omega(x,y)$.
То, что пишете Вы, может обозначено, например $\Omega(x,y,\alpha)$, где $\alpha(t)$ - функция $[t],\{t\}$ или $t$.

vvv369 в сообщении #864184 писал(а):

Если расписать подробно, получается так:

Теперь я понял.

-- Сб май 17, 2014 07:23:06 --

vvv369 в сообщении #862683 писал(а):

Из этого условия, условия (8) и из уравнения (9) получим, что

$2\pi(n)-\pi(\sqrt n) \geqslant \pi(2n) \geqslant 2\pi(n) - 2\pi(\sqrt n) - (\pi(\sqrt{2n})-\pi(\sqrt n))\cdot \left ( \pi(2\sqrt n) - \pi(\sqrt n) - \frac{\pi(\sqrt{2n})-\pi(\sqrt n)-1}{2} \right )$

Левая часть неравенства верна асимпотически:
$2\pi(n)-\pi(\sqrt n)\sim2\frac{n}{\ln n}$.
$\pi(n)\sim\frac{n}{\ln n}$
Правая часть неравенства неверна асимптотически (соотв-но, на компе получается нйти кучу контрпримеров: $n\in [683;683]\cup [1097;1104]\cup[1681;1686]\cup...$)
$\text{правая часть}\sim 2\frac{n}{\ln n} - o(\sqrt{n})-(\frac{\sqrt{2n}}{\ln \sqrt{2n}}-\frac{\sqrt{n}}{\ln \sqrt{n}})(\frac{2\sqrt{n}}{\ln 2\sqrt{n}}+\frac{\sqrt{n}}{2\ln \sqrt{n}}-\frac{\sqrt{2n}}{2\ln \sqrt{2n}}) \sim 2\frac{n}{\ln n}-\frac{2(\sqrt{2}-1)\sqrt{n}}{\ln n}\sqrt{n}(\frac{4}{\ln n}+\frac{1}{\ln n}-\frac{\sqrt{2}}{\ln n})\sim 2\frac{n}{\ln n}-\frac{Cn}{\ln^2n}\sim 2\frac{n}{\ln n}$
Т.е. в пределе получаем соотношение $2\geqslant 1\geqslant 2$
Соотв-но, все, что опирается на правую часть неравенства, не доказано.
Кстати, явных ссылок на теорему 2 в тексте не видно.

[vvv369]

Sonic86 в сообщении #864210 писал(а):

все, что опирается на правую часть неравенства, не доказано.

Нашел, в чем ошибка:
$\sum\limits_{p \le \sqrt n}\Omega(2n,p)- \sum\limits_{p \leqslant \sqrt n} \Omega(n,p)-1 \leqslant \sum\limits_{p \leqslant \sqrt n} \Omega(n,p)+\pi(\sqrt n)$
На самом деле зависимость сложнее и для больших чисел
$\sum\limits_{p \le \sqrt n} \Omega(2n,p)- \sum\limits_{p \leqslant \sqrt n} \Omega(n,p)-1 \geqslant \sum\limits_{p \leqslant \sqrt n} \Omega(n,p)+\pi(\sqrt n)$
Постараюсь сделать новую оценку, если это возможно.
Этот факт кстати свидетельствует в пользу второй гипотезы Харди — Литлвуда, так как тогда уже точно справедливо

$\sum\limits_{p\leqslant \sqrt{x}} \Omega(x+y,p)- \sum\limits_{p\leqslant \sqrt{x}} \Omega(x,p)\geqslant \sum\limits_{p\leqslant \sqrt{y}} \Omega(y,p)+1$ (16)

но в теореме 3 (Брокарда)
$\pi(p_{n+1}^2-p_n^2) -2n -2 \leqslant \pi(p_{n+1}^2)-\pi(p_n^2) \leqslant \pi(p_{n+1}^2-p_n^2) -n -1$
левая часть неверна

Sonic86 в сообщении #864210 писал(а):

Кстати, явных ссылок на теорему 2 в тексте не видно.

Она в дальнейшем нигде не используется

Sonic86 в сообщении #864210 писал(а):

Цитата:

vvv369 в сообщении #862683
писал(а):
Из этого условия, условия (8) и из уравнения (9) получим, что

$2\pi(n)-\pi(\sqrt n) \geqslant \pi(2n) \geqslant 2\pi(n) - 2\pi(\sqrt n) - (\pi(\sqrt{2n})-\pi(\sqrt n))\cdot \left ( \pi(2\sqrt n) - \pi(\sqrt n) - \frac{\pi(\sqrt{2n})-\pi(\sqrt n)-1}{2} \right )$

Левая часть неравенства верна асимпотически:
$2\pi(n)-\pi(\sqrt n)\sim2\frac{n}{\ln n}$.

то есть то, что
$2\pi(n)\geqslant \pi(2n) $ я доказал? В литературе и в интернете я встречал утвержения, что это не доказано.