В сообщении будет рассмотрена функция распределения простых чисел, гипотеза Брокарда, доказана вторая гипотеза Харди — Литлвуда.
Сообщение было изменено, в частности, вместо

было введено обозначение

(как предложил в замечании Sonic86). Из-за большого объема текста часть первоначального сообщения будет вынесена в самостоятельное.
Обозначения:

- количество простых чисел на интервале от 0 до

.

- целая часть от деления
 Краткая теория
Краткая теорияРассмотрим формулу Лежандра
http://mathworld.wolfram.com/LegendresFormula.html
При


(1)
Перегруппируем правые члены сумм в данной формуле с одинаковыми

, получим, что

Введем функцию

(2)
Каждое слагаемое (2) определяет количество чисел на отрезке
![$[0,x]$ $[0,x]$](https://dxdy-03.korotkov.co.uk/f/2/2/d/22dc3894fea3d97bb81528708158ed2c82.png)
, которые делятся на

и не делятся при этом на простые числа меньше

.
Таким образом, (1) можно переписать в виде

(3)
Теорема 1
Для любого натурального числа

справедливо

(4)
Действительно, в правой части уравнения (3) стоит количество чисел на интервале от нуля до

, за исключением единицы.
Так как для любого

на интервале
![$[0,x]$ $[0,x]$](https://dxdy-03.korotkov.co.uk/f/2/2/d/22dc3894fea3d97bb81528708158ed2c82.png)
только само число

не делится на меньшие простые числа, а все остальные числа, в разложении которых есть

, делятся также на другие простые числа меньше

, то для таких простых чисел

(5)
Если

то

Из (3), (4) и (5) следует, что

(6)
где

пробегает все значения на интервале

Теорема 2
Количество простых чисел на отрезке
![$[0,2n]$ $[0,2n]$](https://dxdy-03.korotkov.co.uk/f/6/4/3/643f28db0daaa141f6e2e5394534e41c82.png)

Доказательство
Пусть

- натуральное, запишем функцию распределения в виде

и

Следовательно,

Так как

то

(7)
Рассмотрим

Данная сумма определяет количество чисел, делящихся на простые числа

, и не делящихся на простые числа меньше
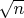
.
Поскольку для любого такого числа выполняется условие

, где

, то такие числа имеют вид либо

, либо

.
Оценим их количество. Заметим, что для любого простого числа

выполняется

, следовательно, на отрезке
![$[0,2n]$ $[0,2n]$](https://dxdy-03.korotkov.co.uk/f/6/4/3/643f28db0daaa141f6e2e5394534e41c82.png)
могут лежать составные числа вида

, только если

Количество простых чисел, для которых

равно

, количество простых чисел

равно

, , следовательно, количество чисел
1.На отрезке
![$[0,n]$ $[0,n]$](https://dxdy-04.korotkov.co.uk/f/7/5/3/7533751ef45cc1d14850770ab9ff241182.png)
вида

равно

2. На отрезке
![$[n+1,2n]$ $[n+1,2n]$](https://dxdy-02.korotkov.co.uk/f/9/d/0/9d028b59836d5d87afe9e59c583fe24982.png)
вида

меньше или равно

Тогда

(8)
Перепишем уравнение (7) в виде:

(9)
Сравним

и

Первая из величин равна количеству чисел на отрезке
![$[n+1,2n]$ $[n+1,2n]$](https://dxdy-02.korotkov.co.uk/f/9/d/0/9d028b59836d5d87afe9e59c583fe24982.png)
, причем таких, которые делятся на простые числа

.
Сумма

показывает количество таких же чисел на отрезке
![$[0,n]$ $[0,n]$](https://dxdy-04.korotkov.co.uk/f/7/5/3/7533751ef45cc1d14850770ab9ff241182.png)
.
Поскольку длина отрезка
![$[0,n]$ $[0,n]$](https://dxdy-04.korotkov.co.uk/f/7/5/3/7533751ef45cc1d14850770ab9ff241182.png)
такая же, как и длина отрезка
![$[n+1,2n]$ $[n+1,2n]$](https://dxdy-02.korotkov.co.uk/f/9/d/0/9d028b59836d5d87afe9e59c583fe24982.png)
, то количество чисел на втором отрезке, делящихся на

, равно или больше на единицу, чем количество таких же чисел на первом отрезке. Кроме того, на отрезке
![$[n+1,2n]$ $[n+1,2n]$](https://dxdy-02.korotkov.co.uk/f/9/d/0/9d028b59836d5d87afe9e59c583fe24982.png)
число

может делиться на

, а единица на отрезке
![$[0,n]$ $[0,n]$](https://dxdy-04.korotkov.co.uk/f/7/5/3/7533751ef45cc1d14850770ab9ff241182.png)
на это

не делится. Следовательно,

Из этого условия, условия (8) и из уравнения (9) получим, что
 Гипотеза Брокарда.
Гипотеза Брокарда.Для любого натурального

между

и

(где

— это

-ое простое число) найдётся хотя бы четыре простых числа
Теорема 3
Для любого натурального

между

и

(где

— это

-ое простое число)

Доказательство
Из функции распределения простых чисел (3) следует, что


Их разность

(10)
Так как

то

С учетом этого перепишем (10)

(11)
Разность

равна количеству чисел на отрезке
![$[p_n^2+1 ,p_{n+1}^2]$ $[p_n^2+1 ,p_{n+1}^2]$](https://dxdy-01.korotkov.co.uk/f/8/c/f/8cf65c6305e7ad92aa6e3e983086413482.png)
, причем таких, которые делятся на простые числа

.
Величина

показывает количество таких же чисел на отрезке
![$[0, p_{n+1}^2-p_n^2]$ $[0, p_{n+1}^2-p_n^2]$](https://dxdy-04.korotkov.co.uk/f/b/b/0/bb02b883bf56aa4df5951db5af52704e82.png)
.
Поскольку длина обоих отрезков одинакова, то количество чисел на отрезке
![$[p_n^2+1 ,p_{n+1}^2]$ $[p_n^2+1 ,p_{n+1}^2]$](https://dxdy-01.korotkov.co.uk/f/8/c/f/8cf65c6305e7ad92aa6e3e983086413482.png)
, делящихся на простое число

, равно или больше на единицу, чем количество таких чисел на другом отрезке. Учтем, что на отрезке
![$[p_n^2+1,p_{n+1}^2]$ $[p_n^2+1,p_{n+1}^2]$](https://dxdy-04.korotkov.co.uk/f/3/0/d/30d331a144c7a6df70f79dbcdcbc279b82.png)
число

может делиться на

, а единица на отрезке
![$[0, p_{n+1}^2-p_n^2]$ $[0, p_{n+1}^2-p_n^2]$](https://dxdy-04.korotkov.co.uk/f/b/b/0/bb02b883bf56aa4df5951db5af52704e82.png)
на такое

не делится.
Количество простых чисел

равно

. Следовательно,

(11)
Тогда из (10) с учетом (11) получим

(12)
Согласно теореме 1

Но так как

и для любого


, то

Следовательно,

и неравенство (12) преобразуется в

Вторая гипотеза Харди — Литлвуда
Докажем, что

Доказательство
Случай

рассмотрен в теореме 2.
Пусть

.
Поскольку

То согласно теореме 1

(13)
Тогда

Или


(14)
Сумма

(15)
Величина

равна количеству чисел на интервале
![$[x,x+y]$ $[x,x+y]$](https://dxdy-04.korotkov.co.uk/f/f/9/8/f985a0db3f11c9989a91a6125edafe6a82.png)
, причем таких, которые делятся на простые числа

. Кроме того, на интервале
![$[x,x+y]$ $[x,x+y]$](https://dxdy-04.korotkov.co.uk/f/f/9/8/f985a0db3f11c9989a91a6125edafe6a82.png)
число

может делиться на

, а единица на интервале
![$[0,y]$ $[0,y]$](https://dxdy-01.korotkov.co.uk/f/4/a/e/4ae5c963e86078d8854b03b72118aa9c82.png)
на такое

не делится.
Величина

показывает количество чисел, которые делятся на простые числа

на интервале
![$[0,y]$ $[0,y]$](https://dxdy-01.korotkov.co.uk/f/4/a/e/4ae5c963e86078d8854b03b72118aa9c82.png)
.
Поскольку длины первого и второго интервалов одинаковы, а по условию

, то

(16)
Так как

то

(17)
Из (14) с учетом (15), (16), (17) окончательно получим

Рассуждая таким же образом для случая

и

получим, что

Случай

также доказывается аналогично