Некоторые свойства формул Абеля

[lasta]

lasta в сообщении #856421 писал(а):

$$(\frac{R^2}{C^2}+\frac{(X^3-Y^3)- Z^{3}_1(R^2-S^2)}{2Z^3}) -(\frac{S^2}{C^2}-\frac{(X^3-Y^3)- Z^{3}_1(R^2-S^2)}{2Z^3})=1.\eqno(13)$$

Опечатка. Правильно

$$(\frac{R^2}{C^2}+\frac{(X^3-Y^3)- Z^{3}_1(R^2-S^2)}{2Z^3}) +(\frac{S^2}{C^2}-\frac{(X^3-Y^3)- Z^{3}_1(R^2-S^2)}{2Z^3})=1.\eqno(13)$$

[lasta]

Для удобства анализа предлагаю объединенную с исправленными опечатками первую часть предполагаемых утверждений.
Формулы Абеля устанавливают,что для любого примитивного решения $(x,y,z)$ уравнения

$$x^p+y^p=z^p,\eqno(1)$$

$p$ простое >2, число $z$ будет произведением $ab$ целых чисел

$$a=x+y\eqno(2)$$

и

$$b=\frac{ x^p+y^p}{x+y}\eqno (3)$$

Можно показать, что число $x+y$ является квадратом.
Предпосылкой доказательства являлась попытка найти противоречия в свойствах степеней уравнения (1) с простым показателем, рассматривая их квадратами (далее в тексте указанные степени будем именовать одним словом – степени). Уравнение (1) было представлено в виде

$$\frac{z^p}{2}-x^p=y^p-\frac{z^p}{2}\eqno(4)$$

Если степени рассматривать как квадраты, то основания квадратов в этом случае будут определяться как $x=\sqrt{x^p}; y=\sqrt{y^p};z=\sqrt{z^p}$. При таком определении степеней, уравнение (4) можно разложить по формулам разностей квадратов. Однако, попытка найти общий алгебраический делитель правой и левой части (4) не удалась. И принцип построения уравнения (4) был перенесен на уравнение Ферма

$$x^p+y^p=1\eqno(5)$$

Согласно этому уравнению, для всех $(p,m)$, если пары чисел $(x,y),(r,s)$ удовлетворяют уравнению (5), то справедливо следующее

$$x^p+y^p=r^m+s^m, \eqno(6)$$

$$s^m-y^p=x^p-r^m. \eqno(7)$$

Ясность соотношений произвольных пар степеней уравнения (5) дает числовая ось

$$\frac{0\text{\qquad\qquad}y^p \text{\qquad}s^m\text{\qquad\qquad} 0.5\text{\qquad\qquad} r^m\text{\qquad}x^p \text{\qquad\qquad}1}{\text{\qquad\qquad}}\rightarrow$$

$$\text{Рис. 1}$$

Согласно (7) и Рис 1 справедливо, что

$$ s^m-y^p=x^p-r^m = \frac{(x^p-y^p)-(r^m-s^m)}{2}, \eqno(8)$$

а

$$x^p = r^m + \frac{(x^p-y^p)-(r^m-s^m)}{2}, \eqno(9)$$

$$ y^p= s^m-\frac{(x^p-y^p)-(r^m-s^m)}{2} \eqno(10)$$

И их сумма

$$x^p+y^p= (r^m + \frac{(x^p-y^p)-(r^m-s^m)}{2})+ ( s^m-\frac{(x^p-y^p)-(r^m-s^m)}{2}) \eqno(11)$$

Абель вывел свои формулы прибавляя и отнимая одинаковые члены в уравнении. При выведение формулы (11) использован такой же прием.
(11) позволяет проведение доказательств важных утверждений для общего случая. Но, согласно правилам форума, (11) преобразуется в уравнение для кубов

$$x^3+y^3= (r^2 + \frac{(x^3-y^3)-(r^2-s^2)}{2})+ ( s^2-\frac{(x^3-y^3)-(r^2-s^2)}{2}) \eqno(12)$$

Числовая ось для кубов и квадратов

$$\frac{0\text{\qquad\qquad}y^3 \text{\qquad}s^2 \text{\qquad\qquad}0.5\text{\qquad\qquad}r^2\text{\qquad}x^3 \text{\qquad\qquad}1}{\text{\qquad\qquad}}\rightarrow$$

$$\text{Рис.2}$$

Решение уравнения (5) для квадратов существует. И если существует рациональное решение этого уравнения для кубов, то основания кубов и квадратов можно выразить натуральными дробями. Тогда,

$$x^3=\frac{X^3}{Z^3}; \text{\qquad\qquad}y^3=\frac{Y^3}{Z^3}\eqno(13)$$

$$r^2=\frac{R^2}{C^2};\text{\qquad\qquad} s^2=\frac{S^2}{C^2} \eqno(14)$$

в соответствии с этим уравнение (12) примет вид

$$x^3+y^3=(\frac{R^2}{C^2}+(\frac{X^3-Y^3}{2Z^3} -\frac{R^2-S^2}{2C^2})) +(\frac{S^2}{C^2}-(\frac{X^3-Y^3}{2Z^3} -\frac{R^2-S^2}{2C^2}))\eqno(15)$$

Пусть $Z>C$. Тогда, $Z$ делится на $C$. То есть $Z^3=C^2 Z^{3}_1$. ( Случай $C>Z$ рассматривается аналогично, но в этом случае $Z$ становится делителем $C$). Тогда,

$$x^3+y^3=(\frac{R^2}{C^2}+\frac{(X^3-Y^3)- Z^3_1(R^2-S^2)}{2Z^3}) +(\frac{S^2}{C^2}-\frac{(X^3-Y^3)- Z^3_1(R^2-S^2)}{2Z^3})\eqno(16)$$

Следовательно,

$$x^3=\frac{R^2}{C^2}+\frac{(X^3-Y^3)- Z^3_1(R^2-S^2)}{2Z^3}\eqno(17)$$

Выражение $(X^3-Y^3)- Z^3_1(R^2-S^2)$ всегда четно. Так как числа $R,S$ для квадратов всегда разной четности, а число $(X^3-Y^3)$ одинаковое по четности с $Z^3_1$, которое в свою очередь одинаковое по четности с $Z$. Следовательно, число $2$ в (16) сокращается.
Знаменатель кубов согласно (13) равен $Z^3$. И в (17) наименьший общий знаменатель должен быть таким же. Значит и с этой стороны подтверждается, что $C^2$ делит $Z^3$.
Следовательно, $Z$ делится на $C$ - знаменатель произвольной $(s , r)$ пары (для показателя $p= 2$) решения уравнения (5).
Частным доказательством является известный факт (который разбирался на форуме), что один из кубов делится на $13$. Для этого числа существует равенство

$$5^2+12^2=13^2 ,$$

которое может быть использовано в качестве числового примера в уравнении (13)

[shwedka]

lasta в сообщении #857057 писал(а):

Формулы Абеля устанавливают,что для любого примитивного решения $(x,y,z)$ уравнения

$$x^p+y^p=z^p,\eqno(1)$$

$p$ простое >2, число $z$ будет произведением $ab$ целых чисел

$$a=x+y\eqno(2)$$

и

$$b=\frac{ x^p+y^p}{x+y}\eqno (3)$$

Чепуха! Формулы Абеля здесь не при чем. Это школьная алгебра.

[lasta]

shwedka в сообщении #857102 писал(а):

Это школьная алгебра.

Уважаемая shwedka!
Большое спасибо за то, что прочитали сообщение!
Полностью согласен с Вами. Смею добавить только то, что вывод Формул Абеля начинается со школьной алгебры. А именно с добавления сокращаемых членов в простейшее уравнение.

[shwedka]

lasta в сообщении #857057 писал(а):

Можно показать, что число $x+y$ является квадратом.

Вы это показать не можете.

[lasta]

shwedka в сообщении #857112 писал(а):

Вы это показать не можете.

shwedka в сообщении #857112 писал(а):

Вы это показать не можете.

Спасибо, что обратили на это внимание. Подготовлена заключительная часть сообщения, где этот факт будет рассмотрен.
и заключительная часть будет опубликована после устранения трудностей понимания данного сообщения. Пишу экспромтом, экономя время, но так его теряю только.

[lasta]

lasta в сообщении #857159 писал(а):

Подготовлена заключительная часть сообщения

Рассмотрим утверждение, что сумма $x+y$ является квадратом. На это утверждение сразу обратили внимание Заслуженный участник Shwedka и участник Binki. Вопрос интересен тем, что его рассмотрение облегчит понимание затруднительных мест изложения первой части сообщения.
Известно, что для любого рационального основания квадрата найдется другое, также рациональное, и такое, что сумма этих квадратов будет также квадратом. Следовательно, шаг последовательности квадратов, может быть каким угодно малым рациональным числом. Поясним существование другого квадрата на формулах. Из равенства

$$s^2_i=2r_id+d^2\eqno(18)$$

Следует, что рациональное основание $r_i$- другого квадрата, составляющего пару для решения уравнения

$$r^2_i+s^2_i=1, \eqno(19)$$

Определяется как

$$r_i=\frac {s^2_i-d^2}{2d},\eqno(20)$$

Все числа правой части (20) рациональны, следовательно $r_i$ также рационален.
Этот элементарный факт является важным моментом. Поэтому, несмотря на такую подробную детализацию, покажем последовательности квадратов, составляющих решение (19) на числовой оси

$$\frac{0\text{\qquad\qquad}s^{2}_i\text{\qquad} s^{2}_3;\text{\quad} s^{2}_2;\text{\quad} s^{2}_1 \text{\qquad\qquad}0.5\text{\qquad\qquad} r^{2}_1;\text{\quad} r^{2}_2;\text{\quad} r^{2}_3\text{\qquad}r^2_i \text{\qquad\qquad}1}{\text{Рис. 3}}\rightarrow$$

В связи как угодно малым шагом последовательности указанных квадратов и симметричности их расположения относительно числа 0,5 , пара кубов (если они существуют), также симметричная, будет отличаться как угодно мало от ближайшей симметричной пары квадратов и в пределе каждый куб будет равен соответствующему квадрату. Но, заключение делать, что сумма $x+y$ является квадратом, пока еще рано. Она все таки еще отличается, пусть бесконечно малым, но отличается. Но, бесконечно малые уже существуют. и это очень хорошо. Они (бесконечно малые) при переходе к (1), если существуют целые решения, могут превратить эти решения в бесконечно большие целые числа.
Далее. Рассмотрим $U^3,V^3$- кубы разложения правой части (1) по формулам Абеля. Известно, что указанные кубы взаимно просты. Если рассматривать (1) для кубов в целых числах, то, не нарушая общности, можно принять, что на $3$ делится правая часть (1). В этом случае $U^3=3 (X+Y)$. Числа (a,b) не взаимно просты. Поэтому если число $a=(X+Y)=3^{3F-1}$, то это квадрат. Во всех других случаях данный квадрат имеет вещественное основание.
Действительно, в этом случае

$$b=(X+Y)^2-3(X+Y)Y+3Y^2=3\cdot(\frac{(X+Y)^2}{3}-(X+Y)Y +Y^2).\eqno(21)$$

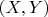
Других делителей (кроме числа 3 и числа $V^3$ - выражения в скобках равенства (21)) не существует, так как числа $(X+Y)$ и $(X,Y)$ взаимно просты.
Тогда, $U^3=3 (X+Y)$. Поэтому если число $a=(X+Y)=3^{3F-1}$, то это квадрат.
Следовательно, в рассматриваемом случае степени разложения по формулам Абеля

$$U^3=3 (X+Y)=3\cdot3^{3F-1}\eqno(23)$$

$$V^3=\frac{(X+Y)^2}{3}-(X+Y)Y +Y^2.\eqno(24)$$

Равенство (23) (24) не противоречит тому, что сумма $(X+Y)$ может быть квадратом. Однако, (как было показано выше) в силу делимости $Z^3$ на произвольный делитель и в силу возможного существования равных остатков кубов и их оснований при их делении на произвольное число не равное 3, указанная сумма оснований будет иметь этот произвольный делитель в виде куба. Поэтому рассматриваемая сумма, может быть квадратом только с вещественным основанием.
Следует особо подчеркнуть, что на указанный произвольный делитель, делиться выбранный конкретный куб. И что все рассуждения по кубам применимы для степеней с любым показателем. Поэтому в результате сделанных выводов по свойствам формул Абеля, вытекает и предполагаемое направление доказательства ВТФ.
Столь подробная детализация объясняется тем, что при доказательстве одного из утверждений в более ранних сообщениях, не принял дельный совет Заслуженного участника Annanova по поиску пересечений двух разных множеств, поскольку посчитал, что сделанные утверждения и так очевидны. Однако, сам Annanova не верил в нахождении в этом направлении каких либо решений.

[shwedka]

Цитата:

Рассмотрим утверждение, что сумма $x+y$ является квадратом.

В результате долгих пустых разговоров,
Ваше утверждение осталось недоказанным. Вы не можете его доказать.

Цитата:

и в пределе каждый куб будет равен соответствующему квадрату.

Бессмысленное заявление. Слова 'в пределе ' и 'каждый' семантически несовместимы.
'соответствие' не установлено.

Цитата:

Рассмотрим $U^3,V^3$- кубы разложения правой части (1) по формулам Абеля. Известно, что указанные кубы взаимно просты.

Не известно! Только в Первом Случае ВТФ3.

Цитата:

бесконечно большие целые числа.

Понятие не определено!

Цитата:

Однако, (как было показано выше) в силу делимости $Z^3$ на произвольный делитель

Показано не было.

Цитата:

Поэтому рассматриваемая сумма, может быть квадратом только с вещественным основанием.

Любое пшоложительноое число-квадрат с вещественным основанием.

К Администрации: Текст ТС представляет собой поток несвязных,недоказанных и часто лишенных смысла заявлений.
Типичный случай для Пургатория.

[Deggial]

shwedka, благодарю.

Тема переносится в Пургаторий по вышеописанной причине.
lasta, предупреждение за размещение на форуме бессвязного, бессмысленного, мутного текста.