Метод наискорейшего спуска.

[Katmandu]

Поскольку сходящаяся минимизирующая последовательность позволяет найти точку минимума функции с произвольной наперед заданной точностью, то следует рассмотреть вопрос о построении такой последовательности.

Поставим следующую задачу: имея точку $x^k \in \mathbb{R}^n $ построить точку $x^{k+1} \in \mathbb{R}^n$
такую, чтобы выполнялось соотношение:

$$ f(x^{k+1}) = x^k + \mu q, q \neq 0$$

,
где $q$ - заданный вектор из $\mathbb{R}^n$, называемый направлением спуска.
Параметр $\mu$ (шаг метода) определяется из условия минимума функции $f(\cdot)$.
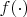
Имеем:

$$ f(x^{k+1}) = f(x^k + \mu q) \equiv \varphi (\mu) = \varphi(0) + \mu \dot \varphi(0) + \frac 1 2 \mu ^2 \ddot \varphi(0), \dot \varphi = \frac {d\varphi} {d\mu} $$

где

$$ \varphi(0) = f(x^k), \dot \varphi(0) = q^T (Ax^k + b), \ddot \varphi(0) = q^TAq$$

В общем то вопрос в том, как так вывели $\dot \varphi(0), \ddot \varphi(0)$

-- 27.04.2014, 11:26 --

Это квадратичная функция, которая дана изначально

$$ f(x) = \frac 1 2 x^TAx + x^Tb $$

-- 27.04.2014, 11:30 --

Можно так расписать, и попробовать взять производную по $\mu$

$$ f(x^k + \mu q) = \frac 1 2 (x^k + \mu q)^TA(x^k+\mu q) + (x^k+\mu q)^Tb = \varphi(\mu) $$

[ewert]

Ну скажем вот это:

$$ \dot \varphi(0) = q^T (Ax^k + b)$$

-- просто стандартное правило дифференцирования сложной функции. В скобках стоит производная $f$ по своему непосредственному аргументу (т.е. градиент), и она умножается на производную того аргумента по параметру $\mu$ (т.е. на вектор $q$). Правда, с транспонированиями лучше бы наоборот, т.к. градиент -- это всё-таки строка. Но тут уж кому арбуз, а кому свиной хрящик.

[Katmandu]

Ну более менее понятно. Иногда операции транспонирования смущают

далее там написано.
Поскольку $\varphi(\mu)$ является квадратным трехчленом относительно $\mu$ с положительным старшим коэффициентом, то у этого трехчлена существует точка минимума $\bar \mu _k$, которая может быть найдена из необходимого условия экстремума $\dot \varphi(\mu) = 0$, откуда получаем:

$$ \bar \mu _k = -\frac {\dot \varphi(0)} {\ddot \varphi(0)} $$

Откуда последняя формула? С каких пор так ищем точку минимума?

[ewert]

Стандартное свойство параболы. Или, если угодно, формула метода Ньютона, который в квадратичном случае вырождается в один шаг.

[Katmandu]

Пусть

$$ f(x) = x^2 + x + 1 $$

Найдем точку минимума

$$ f'(x) = 2x + 1 = 0 $$

Стационарная точка $- \frac 1 2$ - ясно что это минимум.

по формуле выше

$$ \bar x = -\frac {\dot f(0)} {\ddot f(0)} = 1/2 $$

и правда получилось...
Сколько учусь, а формулы такой не припоминаю. Интересно в Фихтенгольце такая формула есть

[ewert]

Метод Ньютона поиска экстремума -- это построение последовательности приближений $\mu_{k+1}=\mu_k-\dfrac{\dot\varphi(\mu_k)}{\ddot\varphi(\mu_k)}$. При определённых условиях эта последовательность сходится к точке экстремума. А для квадратичной функции -- сходится за один шаг, т.е. даёт точку экстремума сразу же.

Причина в том, что эта процедура основана на линеаризации производной, ну а в квадратичном случае эта производная и так линейна.

[Joker_vD]

Трехчлен $ax^2+bx+c$ принимает экстремальное значение в точке $x=-\frac{b}{2a}$, и это написано в школьном учебнике.